| Date | November 2017 | Marks available | 3 | Reference code | 17N.1.sl.TZ0.6 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
The size of a computer screen is the length of its diagonal. Zuzana buys a rectangular computer screen with a size of 68 cm, a height of \(y\) cm and a width of \(x\) cm, as shown in the diagram.
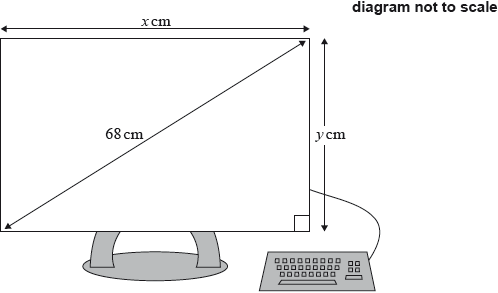
The ratio between the height and the width of the screen is 3:4.
Use this information to write down an equation involving \(x\) and \(y\).
Use this ratio to write down \(y\) in terms of \(x\).
Find the value of \(x\) and of \(y\).
Markscheme
\({x^2} + {y^2} = {68^2}\) (or 4624 or equivalent) (A1) (C1)
[1 mark]
\(\frac{y}{x} = \frac{3}{4}\) (M1)
Note: Award (M1) for a correct equation.
\(y = \frac{3}{4}x{\text{ }}(y = 0.75x)\) (A1) (C2)
[2 marks]
\({x^2} + {\left( {\frac{3}{4}x} \right)^2} = {68^2}{\text{ }}\left( {{\text{or }}{x^2} + \frac{9}{{16}}{x^2} = 4624{\text{ or equivalent}}} \right)\) (M1)
Note: Award (M1) for correct substitution of their expression for \(y\) into their answer to part (a). Accept correct substitution of \(x\) in terms of \(y\).
\(x = 54.4{\text{ (cm), }}y = 40.8{\text{ (cm)}}\) (A1)(ft)(A1)(ft) (C3)
Note: Follow through from parts (a) and (b) as long as \(x > 0\) and \(y > 0\).
[3 marks]

