| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.sl.TZ2.13 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Draw | Question number | 13 | Adapted from | N/A |
Question
The diagram shows part of the graph of a function \(y = f(x)\). The graph passes through point \({\text{A}}(1,{\text{ }}3)\).
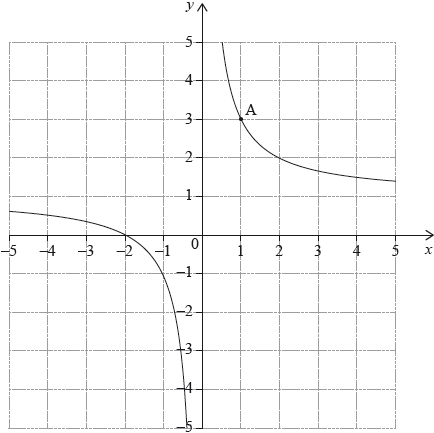
The tangent to the graph of \(y = f(x)\) at A has equation \(y = - 2x + 5\). Let \(N\) be the normal to the graph of \(y = f(x)\) at A.
Write down the value of \(f(1)\).
Find the equation of \(N\). Give your answer in the form \(ax + by + d = 0\) where \(a\), \(b\), \(d \in \mathbb{Z}\).
Draw the line \(N\) on the diagram above.
Markscheme
3 (A1) (C1)
Notes: Accept \(y = 3\)
[1 mark]
\(3 = 0.5(1) + c\)\(\,\,\,\)OR\(\,\,\,\)\(y - 3 = 0.5(x - 1)\) (A1)(A1)
Note: Award (A1) for correct gradient, (A1) for correct substitution of \({\text{A}}(1,{\text{ }}3)\) in the equation of line.
\(x - 2y + 5 = 0\) or any integer multiple (A1)(ft) (C3)
Note: Award (A1)(ft) for their equation correctly rearranged in the indicated form.
The candidate’s answer must be an equation for this mark.
[3 marks]
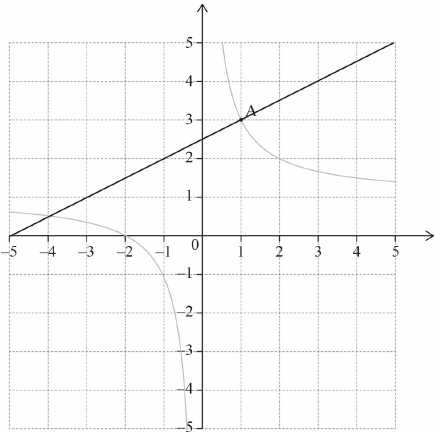(M1)(A1)(ft) (C2)
Note: Award M1) for a straight line, with positive gradient, passing through \((1,{\text{ }}3)\), (A1)(ft) for line (or extension of their line) passing approximately through 2.5 or their intercept with the \(y\)-axis.
[2 marks]
