| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.sl.TZ1.12 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 12 | Adapted from | N/A |
Question
The function \(f\) is of the form \(f(x) = ax + b + \frac{c}{x}\), where \(a\) , \(b\) and \(c\) are positive integers.
Part of the graph of \(y = f(x)\) is shown on the axes below. The graph of the function has its local maximum at \(( - 2,{\text{ }} - 2)\) and its local minimum at \((2,{\text{ }}6)\).
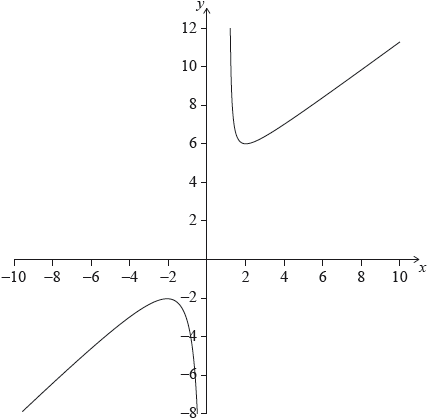
Write down the domain of the function.
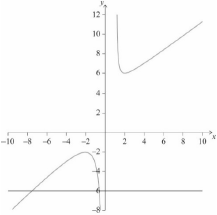
Draw the line \(y = - 6\) on the axes.
Write down the number of solutions to \(f(x) = - 6\).
Find the range of values of \(k\) for which \(f(x) = k\) has no solution.
Markscheme
\((x \in \mathbb{R}),{\text{ }}x \ne 0\) (A2) (C2)
Note: Accept equivalent notation. Award (A1)(A0) for \(y \ne 0\).
Award (A1) for a clear statement that demonstrates understanding of the meaning of domain. For example, \({\text{D}}:( - \infty ,{\text{ }}0) \cup (1,{\text{ }}\infty )\) should be awarded (A1)(A0).
[2 marks]
 (A1) (C1)
(A1) (C1)
Note: The command term “Draw” states: “A ruler (straight edge) should be used for straight lines”; do not accept a freehand \(y = - 6\) line.
[1 mark]
2 (A1)(ft) (C1)
Note: Follow through from part (b)(i).
[1 mark]
\( - 2 < k < 6\) (A1)(A1) (C2)
Note: Award (A1) for both end points correct and (A1) for correct strict inequalities.
Award at most (A1)(A0) if the stated variable is different from \(k\) or \(y\) for example \( - 2 < x < 6\) is (A1)(A0).
[2 marks]

