| Date | November 2017 | Marks available | 4 | Reference code | 17N.2.sl.TZ0.5 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Use, Represent, and Draw | Question number | 5 | Adapted from | N/A |
Question
A function \(f\) is given by \(f(x) = (2x + 2)(5 - {x^2})\).
The graph of the function \(g(x) = {5^x} + 6x - 6\) intersects the graph of \(f\).
Find the exact value of each of the zeros of \(f\).
Expand the expression for \(f(x)\).
Find \(f’(x)\).
Use your answer to part (b)(ii) to find the values of \(x\) for which \(f\) is increasing.
Draw the graph of \(f\) for \( - 3 \leqslant x \leqslant 3\) and \( - 40 \leqslant y \leqslant 20\). Use a scale of 2 cm to represent 1 unit on the \(x\)-axis and 1 cm to represent 5 units on the \(y\)-axis.
Write down the coordinates of the point of intersection.
Markscheme
\( - 1,{\text{ }}\sqrt 5 ,{\text{ }} - \sqrt 5 \) (A1)(A1)(A1)
Note: Award (A1) for –1 and each exact value seen. Award at most (A1)(A0)(A1) for use of 2.23606… instead of \(\sqrt 5 \).
[3 marks]
\(10x - 2{x^3} + 10 - 2{x^2}\) (A1)
Notes: The expansion may be seen in part (b)(ii).
[1 mark]
\(10 - 6{x^2} - 4x\) (A1)(ft)(A1)(ft)(A1)(ft)
Notes: Follow through from part (b)(i). Award (A1)(ft) for each correct term. Award at most (A1)(ft)(A1)(ft)(A0) if extra terms are seen.
[3 marks]
\(10 - 6{x^2} - 4x > 0\) (M1)
Notes: Award (M1) for their \(f’(x) > 0\). Accept equality or weak inequality.
\( - 1.67 < x < 1{\text{ }}\left( { - \frac{5}{3} < x < 1,{\text{ }} - 1.66666 \ldots < x < 1} \right)\) (A1)(ft)(A1)(ft)(G2)
Notes: Award (A1)(ft) for correct endpoints, (A1)(ft) for correct weak or strict inequalities. Follow through from part (b)(ii). Do not award any marks if there is no answer in part (b)(ii).
[3 marks]
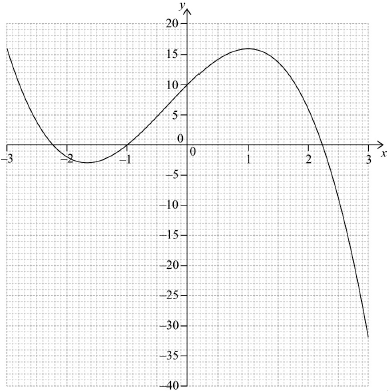(A1)(A1)(ft)(A1)(ft)(A1)
Notes: Award (A1) for correct scale; axes labelled and drawn with a ruler.
Award (A1)(ft) for their correct \(x\)-intercepts in approximately correct location.
Award (A1) for correct minimum and maximum points in approximately correct location.
Award (A1) for a smooth continuous curve with approximate correct shape. The curve should be in the given domain.
Follow through from part (a) for the \(x\)-intercepts.
[4 marks]
\((1.49,{\text{ }}13.9){\text{ }}\left( {(1.48702 \ldots ,{\text{ }}13.8714 \ldots )} \right)\) (G1)(ft)(G1)(ft)
Notes: Award (G1) for 1.49 and (G1) for 13.9 written as a coordinate pair. Award at most (G0)(G1) if parentheses are missing. Accept \(x = 1.49\) and \(y = 13.9\). Follow through from part (b)(i).
[2 marks]
