| Date | November 2013 | Marks available | 2 | Reference code | 13N.2.sl.TZ0.5 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
A particle moves along a straight line such that its velocity, \(v{\text{ m}}{{\text{s}}^{ - 1}}\), is given by \(v(t) = 10t{{\text{e}}^{ - 1.7t}}\), for \(t \geqslant 0\).
On the grid below, sketch the graph of \(v\), for \(0 \leqslant t \leqslant 4\).
Find the distance travelled by the particle in the first three seconds.
Find the velocity of the particle when its acceleration is zero.
Markscheme
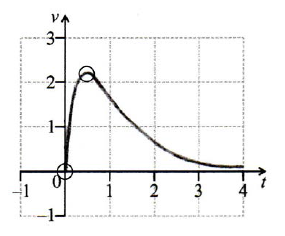 A1A2 N3
A1A2 N3
Notes: Award A1 for approximately correct domain \(0 \leqslant t \leqslant 4\).
The shape must be approximately correct, with maximum skewed left. Only if the shape is approximately correct, award A2 for all the following approximately correct features, in circle of tolerance where drawn (accept seeing correct coordinates for the maximum, even if point outside circle):
Maximum point, passes through origin, asymptotic to \(t\)-axis (but must not touch the axis).
If only two of these features are correct, award A1.
[3 marks]
valid approach (including \(0\) and \(3\)) (M1)
eg \(\int_0^3 {10t{{\text{e}}^{ - 1.7t}}{\text{d}}t,{\text{ }}\int_0^3 {f(x)} } \), area from \(0\) to \(3\) (may be shaded in diagram)
\({\text{distance}} = 3.33{\text{ (m)}}\) A1 N2
[2 marks]
recognizing acceleration is derivative of velocity (R1)
eg \(a = \frac{{{\text{d}}v}}{{{\text{d}}t}}\), attempt to find \(\frac{{{\text{d}}v}}{{{\text{d}}t}}\), reference to maximum on the graph of \(v\)
valid approach to find \(v\) when \(a = 0\) (may be seen on graph) (M1)
eg \(\frac{{{\text{d}}v}}{{{\text{d}}t}} = 0,{\text{ }}10{{\text{e}}^{ - 1.7t}} - 17t{{\text{e}}^{ - 1.7t}} = 0,{\text{ }}t = 0.588\)
\({\text{velocity}} = 2.16{\text{ (m}}{{\text{s}}^{ - 1}})\) A1 N3
Note: Award R1M1A0 for \((0.588, 216)\) if velocity is not identified as final answer
[3 marks]

