| Date | May 2021 | Marks available | 2 | Reference code | 21M.2.SL.TZ1.2 |
| Level | Standard Level | Paper | Paper 2 | Time zone | Time zone 1 |
| Command term | Calculate | Question number | 2 | Adapted from | N/A |
Question
The diagram below shows a circular clockface with centre . The clock’s minute hand has a length of . The clock’s hour hand has a length of .
At pm the endpoint of the minute hand is at point and the endpoint of the hour hand is at point .
Between pm and pm, the endpoint of the minute hand rotates through an angle, , from point to point . This is illustrated in the diagram.
A second clock is illustrated in the diagram below. The clock face has radius with minute and hour hands both of length . The time shown is am. The bottom of the clock face is located above a horizontal bookshelf.
The height, centimetres, of the endpoint of the minute hand above the bookshelf is modelled by the function
where is the angle rotated by the minute hand from am.
The height, centimetres, of the endpoint of the hour hand above the bookshelf is modelled by the function
where is the angle in degrees rotated by the minute hand from am.
Find the size of angle in degrees.
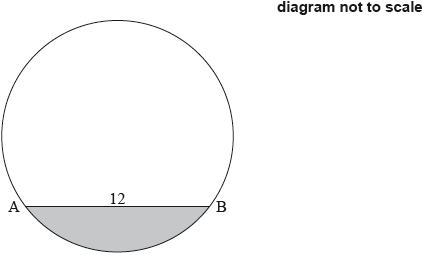
Find the distance between points and .
Find the size of angle in degrees.
Calculate the length of arc .
Calculate the area of the shaded sector, .
Write down the height of the endpoint of the minute hand above the bookshelf at am.
Find the value of when .
Write down the amplitude of .
The endpoints of the minute hand and hour hand meet when .
Find the smallest possible value of .
Markscheme
OR (M1)
A1
[2 marks]
substitution in cosine rule (M1)
(A1)
A1
Note: Follow through marks in part (b) are contingent on working seen.
[3 marks]
(M1)
A1
[2 marks]
substitution into the formula for arc length (M1)
OR
A1
[2 marks]
substitution into the area of a sector (M1)
OR
A1
[2 marks]
A1
[1 mark]
correct substitution (M1)
A1
[2 marks]
A1
[1 mark]
EITHER
(M1)
OR
(M1)
Note: Award M1 for equating the functions. Accept a sketch of and with point(s) of intersection marked.
THEN
A1
Note: The answer is incorrect but the correct method is implicit. Award (M1)A0.
[2 marks]