IB Questionbank

User interface language: English | Español

Date	November 2016	Marks available	3	Reference code	16N.1.AHL.TZ0.H_11
Level	Additional Higher Level	Paper	Paper 1	Time zone	Time zone 0
Command term	Sketch	Question number	H_11	Adapted from	N/A

Question

Let $y = {{\text{e}}^x}\sin x$ .

Consider the function $f$ defined by $f(x) = {{\text{e}}^x}\sin x,{\text{ }}0 \leqslant x \leqslant \pi$ .

The curvature at any point $(x,{\text{ }}y)$ on a graph is defined as $\kappa = \frac{{\left| {\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}}} \right|}}{{{{\left( {1 + {{\left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)}^2}} \right)}^{\frac{3}{2}}}}}$ .

Find an expression for $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ .

[2]

Show that $\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x$ .

[2]

Show that the function $f$ has a local maximum value when $x = \frac{{3\pi }}{4}$ .

[2]

Find the $x$ -coordinate of the point of inflexion of the graph of $f$ .

[2]

Sketch the graph of $f$ , clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.

[3]

Find the area of the region enclosed by the graph of $f$ and the $x$ -axis.

[6]

Find the value of the curvature of the graph of $f$ at the local maximum point.

[3]

Find the value $\kappa$ for $x = \frac{\pi }{2}$ and comment on its meaning with respect to the shape of the graph.

[2]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

$\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^x}\sin x + {{\text{e}}^x}\cos x{\text{ }}\left( { = {{\text{e}}^x}(\sin x + \cos x)} \right)$ M1A1

[2 marks]

$\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = {{\text{e}}^x}(\sin x + \cos x) + {{\text{e}}^x}(\cos x - \sin x)$ M1A1

$= 2{{\text{e}}^x}\cos x$ AG

[2 marks]

$\frac{{{\text{d}}y}}{{{\text{d}}x}} = {{\text{e}}^{\frac{{3\pi }}{4}}}\left( {\sin \frac{{3\pi }}{4} + \cos \frac{{3\pi }}{4}} \right) = 0$ R1

$\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} < 0$ R1

hence maximum at $x = \frac{{3\pi }}{4}$ AG

[2 marks]

$\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 0 \Rightarrow 2{{\text{e}}^x}\cos x = 0$ M1

$\Rightarrow x = \frac{\pi }{2}$ A1

Note: Award M1A0 if extra zeros are seen.

[2 marks]

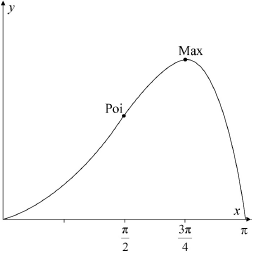
N16/5/MATHL/HP1/ENG/TZ0/11.e/M

correct shape and correct domain A1

max at $x = \frac{{3\pi }}{4}$ , point of inflexion at $x = \frac{\pi }{2}$ A1

zeros at $x = 0$ and $x = \pi$ A1

Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.

[3 marks]

EITHER

$\int_0^x {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi - \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} }$ M1A1

$\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [{{\text{e}}^x}\sin x]_0^\pi - \left( {[{{\text{e}}^x}\cos x]_0^x + \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)}$ A1

$\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ - {{\text{e}}^x}\cos x]_0^\pi + \int_0^\pi {{{\text{e}}^x}\cos x{\text{d}}x} }$ M1A1

$\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = [ - {{\text{e}}^x}\cos x]} _0^\pi + \left( {[{{\text{e}}^x}\sin x]_0^\pi - \int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x} } \right)$ A1

THEN

$\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}\left( {[{{\text{e}}^x}\sin x]_0^x - [{{\text{e}}^x}\cos x]_0^x} \right)}$ M1A1

$\int_0^\pi {{{\text{e}}^x}\sin x{\text{d}}x = \frac{1}{2}({{\text{e}}^x} + 1)}$ A1

[6 marks]

$\frac{{{\text{d}}y}}{{{\text{d}}x}} = 0$ (A1)

$\frac{{{d^2}y}}{{d{x^2}}} = 2{e^{\frac{{3\pi }}{4}}}\cos \frac{{3\pi }}{4} = - \sqrt 2 {e^{\frac{{3\pi }}{4}}}$ (A1)

$\kappa = \frac{{\left| { - \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}} \right|}}{1} = \sqrt 2 {{\text{e}}^{\frac{{3\pi }}{4}}}$ A1

[3 marks]

$\kappa = 0$ A1

the graph is approximated by a straight line R1

[2 marks]

Examiners report

[N/A]

Syllabus sections

Topic 5—Calculus » AHL 5.16—Eulers method for 1st order DEs

Show 40 related questions

SPM.3.AHL.TZ0.2d.iii:
Use further iterations of Euler’s method to find the long-term population for each species of squirrel from these initial values.
SPM.3.AHL.TZ0.2f:
Given that the equilibrium point at (800, 600) is a saddle point, sketch the phase portrait for $x$ ≥ 0 , $y$ ≥ 0 on the same axes used in part (e).
SPM.3.AHL.TZ0.2a.i:
Find the equilibrium population of brown squirrels suggested by this model.
SPM.3.AHL.TZ0.2d.i:
Write down the expressions for ${x_{n + 1}}$ and ${y_{n + 1}}$ that the conservationists will use.
SPM.3.AHL.TZ0.2d.iv:
Use the same method to find the long-term populations of squirrels when the initial populations are $x = 400$ , $y = 100$ .
SPM.3.AHL.TZ0.2a.ii:
Explain why the population of squirrels is increasing for values of $x$ less than this value.
16N.1.AHL.TZ0.H_11c:
Show that the function $f$ has a local maximum value when $x = \frac{{3\pi }}{4}$ .
16N.1.AHL.TZ0.H_11d:
Find the $x$ -coordinate of the point of inflexion of the graph of $f$ .
SPM.3.AHL.TZ0.2c.ii:
Write down the general solution of $\frac{{{\text{d}}y}}{{{\text{d}}t}} = 3y$ .
SPM.3.AHL.TZ0.2b.ii:
Find the other three equilibrium points.
16N.1.AHL.TZ0.H_11h:
Find the value $\kappa$ for $x = \frac{\pi }{2}$ and comment on its meaning with respect to the shape of the graph.
16N.1.AHL.TZ0.H_11g:
Find the value of the curvature of the graph of $f$ at the local maximum point.
16N.1.AHL.TZ0.H_11f:
Find the area of the region enclosed by the graph of $f$ and the $x$ -axis.
SPM.3.AHL.TZ0.2d.ii:
Given that the initial populations are $x = 100$ , $y = 100$ , find the populations of each species of squirrel when $t = 1$ .
SPM.3.AHL.TZ0.2e:
Use Euler’s method with step length 0.2 to sketch, on the same axes, the approximate trajectories for the populations with the following initial populations.

(i) $x = 1000$ , $y = 1500$

(ii) $x = 1500$ , $y = 1000$
SPM.3.AHL.TZ0.2c.i:
By using separation of variables, show that the general solution of $\frac{{{\text{d}}x}}{{{\text{d}}t}} = 2x$ is $x = A{{\text{e}}^{2t}}$ .
16N.1.AHL.TZ0.H_11b:
Show that $\frac{{{{\text{d}}^2}y}}{{{\text{d}}{x^2}}} = 2{{\text{e}}^x}\cos x$ .
SPM.3.AHL.TZ0.2c.iii:
If both populations contain 10 squirrels at $t = 0$ use the solutions to parts (c) (i) and (ii) to estimate the number of black and brown squirrels when $t = 0.2$ . Give your answers to the nearest whole numbers.
SPM.3.AHL.TZ0.2b.i:
Verify that $x = 800$ , $y = 600$ is an equilibrium point.
16N.1.AHL.TZ0.H_11a:
Find an expression for $\frac{{{\text{d}}y}}{{{\text{d}}x}}$ .
21M.2.AHL.TZ1.7d:
Find the non-zero equilibrium point for the populations of rabbits and foxes.
21M.2.AHL.TZ1.7c.i:
point $A$ .
21M.2.AHL.TZ1.7c.ii:
point $B$ .
21M.2.AHL.TZ1.7b:
(i) the population of rabbits 1 year after the foxes were introduced.

(ii) the population of foxes 1 year after the foxes were introduced.
21M.3.AHL.TZ2.2e.i:
Write down expressions for $M_{n + 1}$ and $S_{n + 1}$ in terms of $M_{n}$ and $S_{n}$ .
21M.3.AHL.TZ2.2e.ii:
Use Euler’s method to find an estimate for the mackerel population density after one year.
EXN.2.AHL.TZ0.4b:
Show that $r \approx \frac{N (n + 1) - N (n)}{N (n)}$
EXN.2.AHL.TZ0.4c:
Hence find three approximations for the value of $r$ .
21N.3.AHL.TZ0.2a.i:
Find the equation of the regression line of $h$ on $t$ .
21N.3.AHL.TZ0.2a.ii:
Interpret the meaning of parameter $a$ in the context of the model.
21N.3.AHL.TZ0.2a.iii:
Suggest why Eva’s use of the linear regression equation in this way could be unreliable.
21N.3.AHL.TZ0.2b.i:
Find the equation of the least squares quadratic regression curve.
21N.3.AHL.TZ0.2b.ii:
Find the value of $k$ .
21N.3.AHL.TZ0.2b.iii:
Hence, write down a suitable domain for Eva’s function $h (t) = p t^{2} + q t + r$ .
21N.3.AHL.TZ0.2c:
Show that $\frac{d h}{d t} = - R^{2} \sqrt{70 560 h}$ .
21N.3.AHL.TZ0.2d:
By solving the differential equation $\frac{d h}{d t} = - R^{2} \sqrt{70 560 h}$ , show that the general solution is given by $h = 17 640 {(c - R^{2} t)}^{2}$ , where $c \in ℝ$ .
21N.3.AHL.TZ0.2e:
Use the general solution from part (d) and the initial condition $h (0) = 3.2$ to predict the value of $T$ .
21N.3.AHL.TZ0.2f:
Find this new height.
21N.3.AHL.TZ0.2g.i:
Show that $\frac{d H}{d t} \approx 0.2514 - 0.009873 t - 0.1405 \sqrt{H}$ , where $0 \leq t \leq T$ .
21N.3.AHL.TZ0.2g.ii:
Use Euler’s method with a step length of $0.5$ minutes to estimate the maximum value of $H$ .

Hide related questions

Topic 5—Calculus

Question

Markscheme

Examiners report

Syllabus sections

View options