| Date | November 2016 | Marks available | 2 | Reference code | 16N.1.AHL.TZ0.H_11 |
| Level | Additional Higher Level | Paper | Paper 1 | Time zone | Time zone 0 |
| Command term | Show that | Question number | H_11 | Adapted from | N/A |
Question
Let .
Consider the function defined by .
The curvature at any point on a graph is defined as .
Find an expression for .
Show that .
Show that the function has a local maximum value when .
Find the -coordinate of the point of inflexion of the graph of .
Sketch the graph of , clearly indicating the position of the local maximum point, the point of inflexion and the axes intercepts.
Find the area of the region enclosed by the graph of and the -axis.
Find the value of the curvature of the graph of at the local maximum point.
Find the value for and comment on its meaning with respect to the shape of the graph.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
M1A1
[2 marks]
M1A1
AG
[2 marks]
R1
R1
hence maximum at AG
[2 marks]
M1
A1
Note: Award M1A0 if extra zeros are seen.
[2 marks]
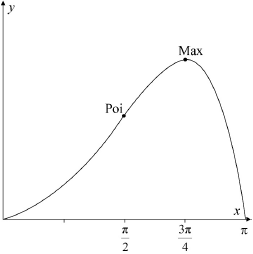
correct shape and correct domain A1
max at , point of inflexion at A1
zeros at and A1
Note: Penalize incorrect domain with first A mark; allow FT from (d) on extra points of inflexion.
[3 marks]
EITHER
M1A1
A1
OR
M1A1
A1
THEN
M1A1
A1
[6 marks]
(A1)
(A1)
A1
[3 marks]
A1
the graph is approximated by a straight line R1
[2 marks]

