IB Questionbank

User interface language: English | Español

Date	May 2017	Marks available	2	Reference code	17M.2.SL.TZ2.S_6
Level	Standard Level	Paper	Paper 2	Time zone	Time zone 2
Command term	Show that	Question number	S_6	Adapted from	N/A

Question

Let $f(x) = {x^2} - 1$ and $g(x) = {x^2} - 2$ , for $x \in \mathbb{R}$ .

Show that $(f \circ g)(x) = {x^4} - 4{x^2} + 3$ .

[2]

On the following grid, sketch the graph of $(f \circ g)(x)$ , for $0 \leqslant x \leqslant 2.25$ .

M17/5/MATME/SP2/ENG/TZ2/06.b

[3]

The equation $(f \circ g)(x) = k$ has exactly two solutions, for $0 \leqslant x \leqslant 2.25$ . Find the possible values of $k$ .

[3]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

attempt to form composite in either order (M1)

eg $\,\,\,\,\,$ $f({x^2} - 2),{\text{ }}{({x^2} - 1)^2} - 2$

$({x^4} - 4{x^2} + 4) - 1$ A1

$(f \circ g)(x) = {x^4} - 4{x^2} + 3$ AG N0

[2 marks]

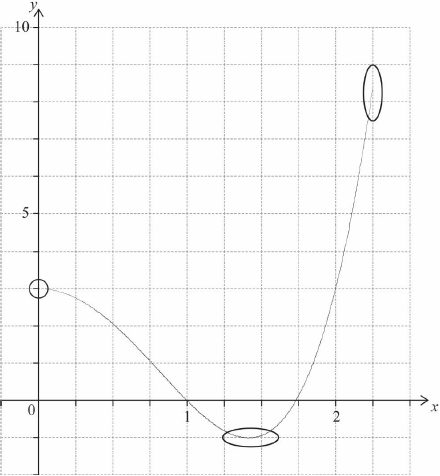M17/5/MATME/SP2/ENG/TZ2/06.b/M A1

A1A1 N3

Note: Award A1 for approximately correct shape which changes from concave down to concave up. Only if this A1 is awarded, award the following:

A1 for left hand endpoint in circle and right hand endpoint in oval,

A1 for minimum in oval.

[3 marks]

evidence of identifying max/min as relevant points (M1)

eg $\,\,\,\,\,$ $x = 0,{\text{ }}1.41421,{\text{ }}y = - 1,{\text{ }}3$

correct interval (inclusion/exclusion of endpoints must be correct) A2 N3

eg $\,\,\,\,\,$ $- 1 < k \leqslant 3,{\text{ }}\left] { - 1,{\text{ 3}}} \right],{\text{ }}( - 1,{\text{ }}3]$

[3 marks]

Examiners report

[N/A]

Syllabus sections

Topic 2—Functions » SL 2.5—Composite functions, identity, finding inverse

Show 49 related questions

22M.1.SL.TZ2.1c:
Find the value of $x$ such that $f (x) = 0$ .
22M.2.SL.TZ1.8b.i:
Find $f^{- 1} (x)$ .
18N.2.AHL.TZ0.H_9c.i:
sketch the graph of $y = f\left( x \right)$ , showing clearly any axis intercepts and giving the equations of any asymptotes.
21N.1.SL.TZ0.5b:
Find $f (4)$ .
21N.1.AHL.TZ0.2a.i:
the vertical asymptote of the graph of $f$ .
21N.1.AHL.TZ0.2a.ii:
the horizontal asymptote of the graph of $f$ .
21N.1.AHL.TZ0.2c:
Sketch the graph of $f$ on the axes below.
18N.3.AHL.TZ0.Hsrg_4b:
State with a reason whether or not $f$ and $g$ commute.
21N.1.SL.TZ0.5a:
Write down the value of $f' (4)$ .
21N.1.AHL.TZ0.2b.ii:
the $y$ -axis.
17N.1.SL.TZ0.S_5a:
Find $(g \circ f)(x)$ .
18N.2.AHL.TZ0.H_9c.ii:
sketch the graph of $y = {f^{ - 1}}\left( x \right)$ , showing clearly any axis intercepts and giving the equations of any asymptotes.
19N.2.SL.TZ0.S_3b:
Let ${\text{C}}$ be a point on the graph of $h$ . The tangent to the graph of $h$ at ${\text{C}}$ is parallel to the graph of $f$ .

Find the $x$ -coordinate of ${\text{C}}$ .
19N.2.SL.TZ0.S_3a:
Find $h\left( x \right)$ .
17N.1.SL.TZ0.S_5b:
Given that $\mathop {\lim }\limits_{x \to + \infty } (g \circ f)(x) = - 3$ , find the value of $b$ .
18N.3.AHL.TZ0.Hsrg_4c:
Find the inverse of $f$ .
22M.1.SL.TZ2.1b:
Find $(f \circ g) (0)$ .
EXN.1.SL.TZ0.8c:
Find an expression for $f^{- 1} (x)$ , stating its domain.
22M.1.AHL.TZ2.11c:
Given that $(h \circ g) (a) = \frac{π}{4}$ , find the value of $a$ .

Give your answer in the form $p + \frac{q}{2} \sqrt{r}$ , where $p, q, r \in ℤ^{+}$ .
22M.2.SL.TZ1.8b.ii:
Using an algebraic approach, show that the graph of $f^{- 1}$ is obtained by a reflection of the graph of $f$ in the $y$ -axis followed by a reflection in the $x$ -axis.
20N.2.SL.TZ0.S_4b.i:
Solve the equation $(f \circ g) (x) = x$ .
21M.1.SL.TZ1.1a.i:
Write down the value of $f (2)$ .
21M.1.SL.TZ1.1a.ii:
Write down the value of $(f \circ f) (2)$ .
18N.2.AHL.TZ0.H_9d:
Hence, or otherwise, solve the inequality $f\left( x \right) > {f^{ - 1}}\left( x \right)$ .
18N.3.AHL.TZ0.Hsrg_4a.i:
Find $\left( {f \circ g} \right)\left( {\left( {x{\text{,}}\,\,y} \right)} \right)$ .
SPM.1.SL.TZ0.5b:
Given that ${\left( {g \circ f} \right)^{ - 1}}\left( a \right) = 4$ , find the value of $a$ .
18N.3.AHL.TZ0.Hsrg_4a.ii:
Find $\left( {g \circ f} \right)\left( {\left( {x{\text{,}}\,\,y} \right)} \right)$ .
20N.2.SL.TZ0.S_4b.ii:
Hence or otherwise, given that $g (2 a) = f^{- 1} (2 a)$ , find the value of $a$ .
EXN.1.SL.TZ0.5:
The functions $f$ and $g$ are defined for $x \in ℝ$ by $f (x) = x - 2$ and $g (x) = a x + b$ , where $a, b \in ℝ$ .

Given that $(f \circ g) (2) = - 3$ and $(g \circ f) (1) = 5$ , find the value of $a$ and the value of $b$ .
21M.2.AHL.TZ2.12d:
Find an expression for $g^{- 1} (x)$ , justifying your answer.
EXN.1.SL.TZ0.8b:
State the range of $f$ .
EXN.2.SL.TZ0.2c:
Arc $APB$ is twice the length of chord $[AB]$ .

Find the value of $θ$ .
21M.2.SL.TZ2.5b:
Given that $(g \circ f) (x) \leq 0$ for all $x \in ℝ$ , determine the set of possible values for $c$ .
SPM.1.SL.TZ0.5a:
Show that $\left( {g \circ f} \right)\left( x \right) = 2x + 11$ .
21N.1.AHL.TZ0.2d:
The function $g$ is defined by $g (x) = \frac{a x + 4}{3 - x}$ , where $x \in ℝ, x \neq 3$ and $a \in ℝ$ .

Given that $g (x) = g^{- 1} (x)$ , determine the value of $a$ .
22M.1.SL.TZ1.4a:
Find $(f \circ g) (x)$ .
21N.1.SL.TZ0.8b:
Write down an expression for $f^{- 1} (x)$ .
21N.1.AHL.TZ0.2b.i:
the $x$ -axis.
21N.1.SL.TZ0.8c:
Find the value of $f^{- 1} (\sqrt{32})$ .
21N.1.SL.TZ0.5c:
Find $h (4)$ .
16N.3.AHL.TZ0.Hsrg_2a:
(i) Sketch the graph of $y = f(x)$ and hence justify whether or not $f$ is a bijection.

(ii) Show that $A$ is a group under the binary operation of multiplication.

(iii) Give a reason why $B$ is not a group under the binary operation of multiplication.

(iv) Find an example to show that $f(a \times b) = f(a) \times f(b)$ is not satisfied for all $a,{\text{ }}b \in A$ .
20N.2.SL.TZ0.S_4a:
Find $(f \circ g) (x)$ .
16N.3.AHL.TZ0.Hsrg_2b:
(i) Sketch the graph of $y = g(x)$ and hence justify whether or not $g$ is a bijection.

(ii) Show that $g(a + b) = g(a) \times g(b)$ for all $a,{\text{ }}b \in \mathbb{R}$ .

(iii) Given that $\{ \mathbb{R},{\text{ }} + \}$ and $\{ D,{\text{ }} \times \}$ are both groups, explain whether or not they are isomorphic.
EXN.1.SL.TZ0.8d:
Find the coordinates of the point(s) where the graphs of $y = f (x)$ and $y = f^{- 1} (x)$ intersect.
18N.2.AHL.TZ0.H_9b:
Hence, or otherwise, find the coordinates of the point of inflexion on the graph of $y = f\left( x \right)$ .
21N.1.SL.TZ0.5d:
Hence find the equation of the tangent to the graph of $h$ at $x = 4$ .
21N.1.SL.TZ0.8a:
Show that $a = 8$ .
21N.1.SL.TZ0.8d.ii:
Find the value of $p$ and the value of $q$ .
21N.1.SL.TZ0.8d.i:
Show that $27, p, q$ and $125$ are four consecutive terms in a geometric sequence.

Hide related questions

Topic 2—Functions

Question

Markscheme

Examiners report

Syllabus sections

View options