DP Physics Questionbank

4.1 – Oscillations
| Path: |
Description
Nature of science:
Models: Oscillations play a great part in our lives, from the tides to the motion of the swinging pendulum that once governed our perception of time. General principles govern this area of physics, from water waves in the deep ocean or the oscillations of a car suspension system. This introduction to the topic reminds us that not all oscillations are isochronous. However, the simple harmonic oscillator is of great importance to physicists because all periodic oscillations can be described through the mathematics of simple harmonic motion. (1.10)
Understandings:
- Simple harmonic oscillations
- Time period, frequency, amplitude, displacement and phase difference
- Conditions for simple harmonic motion
Applications and skills:
- Qualitatively describing the energy changes taking place during one cycle of an oscillation
- Sketching and interpreting graphs of simple harmonic motion examples
Guidance:
- Graphs describing simple harmonic motion should include displacement–time, velocity–time, acceleration–time and acceleration–displacement
- Students are expected to understand the significance of the negative sign in the relationship:
Data booklet reference:
International-mindedness:
- Oscillations are used to define the time systems on which nations agree so that the world can be kept in synchronization. This impacts most areas of our lives including the provision of electricity, travel and location-determining devices and all microelectronics.
Theory of knowledge:
- The harmonic oscillator is a paradigm for modelling where a simple equation is used to describe a complex phenomenon. How do scientists know when a simple model is not detailed enough for their requirements?
Utilization:
- Isochronous oscillations can be used to measure time
- Many systems can approximate simple harmonic motion: mass on a spring, fluid in U-tube, models of icebergs oscillating vertically in the ocean, and motion of a sphere rolling in a concave mirror
- Simple harmonic motion is frequently found in the context of mechanics (seePhysics topic 2)
Aims:
- Aim 6: experiments could include (but are not limited to): mass on a spring; simple pendulum; motion on a curved air track
- Aim 7: IT skills can be used to model the simple harmonic motion defining equation; this gives valuable insight into the meaning of the equation itself
Directly related questions
-
16N.1.SL.TZ0.14:
A particle oscillates with simple harmonic motion (shm) of period T. Which graph shows the variation with time of the kinetic energy of the particle?
-
16N.1.SL.TZ0.13:
A body undergoes one oscillation of simple harmonic motion (shm). What is correct for the direction of the acceleration of the body and the direction of its velocity?
A. Always opposite
B. Opposite for half a period
C. Opposite for a quarter of a period
D. Never opposite -
17M.1.SL.TZ1.13:
A particle undergoes simple harmonic motion (SHM). The graph shows the variation of velocity v of the particle with time t.
What is the variation with time of the acceleration a of the particle?
- 17M.1.SL.TZ1.15: Two pulses are travelling towards each other. What is a possible pulse shape when the pulses...
- 17M.1.SL.TZ2.13: In simple harmonic oscillations which two quantities always have opposite directions? A....
-
17M.2.HL.TZ2.2a:
Outline the conditions necessary for simple harmonic motion (SHM) to occur.
- 20N.1.SL.TZ0.14: An object moves with simple harmonic motion. The acceleration of the object is A. ...
-
20N.1.SL.TZ0.15:
A travelling wave has a frequency of . The closest distance between two points on the wave that have a phase difference of is . What is the speed of the wave?
A.
B.
C.
D.
-
20N.2.HL.TZ0.7a:
Outline why the cylinder performs simple harmonic motion when released.
-
17N.1.SL.TZ0.12:
The graph shows the variation with time t of the velocity v of an object undergoing simple harmonic motion (SHM). At which velocity does the displacement from the mean position take a maximum positive value?
-
17N.1.HL.TZ0.11:
The graph shows the variation with position s of the displacement x of a wave undergoing simple harmonic motion (SHM).
What is the magnitude of the velocity at the displacements X, Y and Z?
- 21M.2.HL.TZ1.8b.ii: Sketch a graph to show how the acceleration of point P varies with its displacement from the rest...
-
21M.1.SL.TZ1.13:
An object performs simple harmonic motion (shm). The graph shows how the velocity v of the object varies with time t.
The displacement of the object is x and its acceleration is a. What is the variation of x with t and the variation of a with t?
-
21M.1.SL.TZ2.13:
The bob of a pendulum has an initial displacement to the right. The bob is released and allowed to oscillate. The graph shows how the displacement varies with time. At which point is the velocity of the bob at its maximum magnitude directed towards the left?
- 21M.2.SL.TZ1.6b.ii: Sketch a graph to show how the acceleration of point P varies with its displacement from the rest...
- 18M.1.SL.TZ1.14: Two travelling waves are moving through a medium. The diagram shows, for a point in the medium,...
- 18M.1.SL.TZ1.16: A system that is subject to a restoring force oscillates about an equilibrium position. For the...
-
18M.1.SL.TZ1.17:
A particle is displaced from rest and released at time t = 0. It performs simple harmonic motion (SHM). Which graph shows the variation with time of the kinetic energy Ek of the particle?
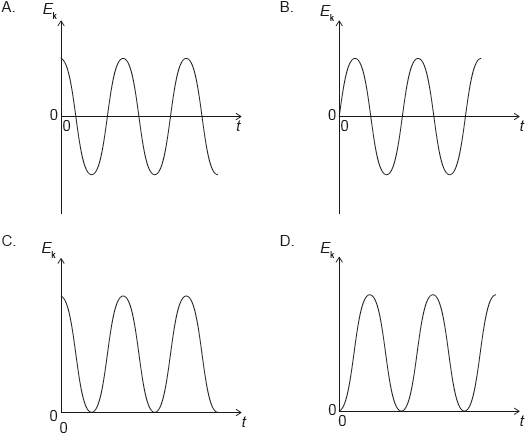
-
18M.1.SL.TZ2.15:
What is true about the acceleration of a particle that is oscillating with simple harmonic motion (SHM)?
A. It is in the opposite direction to its velocity
B. It is decreasing when the potential energy is increasing
C. It is proportional to the frequency of the oscillation
D. It is at a minimum when the velocity is at a maximum
- 18M.1.SL.TZ2.14: Two sound waves from a point source on the ground travel through the ground to a detector. The...
-
18M.2.HL.TZ2.1d.i:
Outline why the ball will perform simple harmonic oscillations about the equilibrium position.
-
21N.1.SL.TZ0.13:
A particle undergoes simple harmonic motion of amplitude and frequency . What is the average speed of the particle during one oscillation?
A.B.
C.
D.
-
21N.2.SL.TZ0.3b.i:
State the phase difference between the two waves.
-
21N.2.HL.TZ0.2c.i:
State the phase difference between the two waves.
- 18N.2.SL.TZ0.4c.i: Demonstrate, using a second ray, that the image appears to come from the position indicated.
-
18N.1.SL.TZ0.13:
A particle moving in a circle completes 5 revolutions in 3 s. What is the frequency?
A. Hz
B. Hz
C. Hz
D. Hz
- 18N.2.HL.TZ0.4c.i: Demonstrate, using a second ray, that the image appears to come from the position indicated.
- 22M.1.SL.TZ2.14: A particle is moving in a straight line with an acceleration proportional to its displacement and...
- 22M.1.HL.TZ2.12: A particle undergoes simple harmonic motion. Which quantities of the motion can be simultaneously...
- 22M.2.HL.TZ2.6a.i: Calculate the frequency of the oscillation for both tests.
-
19M.2.HL.TZ2.3b:
The wave is incident at point Q on the metal–air boundary. The wave makes an angle of 54° with the normal at Q. The speed of sound in the metal is 6010 m s–1 and the speed of sound in air is 340 m s–1. Calculate the angle between the normal at Q and the direction of the wave in air.
-
19M.2.SL.TZ2.3b:
The wave is incident at point Q on the metal–air boundary. The wave makes an angle of 54° with the normal at Q. The speed of sound in the metal is 6010 m s–1 and the speed of sound in air is 340 m s–1. Calculate the angle between the normal at Q and the direction of the wave in air.
-
19M.1.SL.TZ2.14:
Object P moves vertically with simple harmonic motion (shm). Object Q moves in a vertical circle with a uniform speed. P and Q have the same time period T. When P is at the top of its motion, Q is at the bottom of its motion.
What is the interval between successive times when the acceleration of P is equal and opposite to the acceleration of Q?
A.
B.
C.
D. T
- 19M.1.SL.TZ2.13: The graph shows the variation of the displacement of a wave with distance along the wave. The...
-
19M.1.SL.TZ1.15:
Which graph shows the variation with time t of the kinetic energy (KE) of an object undergoing simple harmonic motion (shm) of period T?
- 19M.1.SL.TZ1.18: A string fixed at both ends vibrates in the first harmonic with frequency 400 Hz. The speed of...
-
19M.1.SL.TZ1.14:
A particle performs simple harmonic motion (shm). What is the phase difference between the displacement and the acceleration of the particle?
A. 0
B.
C.
D.
- 19N.2.SL.TZ0.3b: The graph also shows the displacement of two particles, P and Q, in the medium at t = 0. State...
- 19N.1.SL.TZ0.12: The motion of an object is described by the equation acceleration ∝ − displacement. What is the...
