IB Questionbank

User interface language: English | Español

Date	November 2020	Marks available	1	Reference code	20N.2.HL.TZ0.7
Level	Higher level	Paper	Paper 2	Time zone	0 - no time zone
Command term	Outline	Question number	7	Adapted from	N/A

Question

A vertical solid cylinder of uniform cross-sectional area $A$ floats in water. The cylinder is partially submerged. When the cylinder floats at rest, a mark is aligned with the water surface. The cylinder is pushed vertically downwards so that the mark is a distance $x$ below the water surface.

At time $t = 0$ the cylinder is released. The resultant vertical force $F$ on the cylinder is related to the displacement $x$ of the mark by

$F = - ρ A g x$

where $ρ$ is the density of water.

The cylinder was initially pushed down a distance $x = 0.250 m$ .

Outline why the cylinder performs simple harmonic motion when released.

[1]

The mass of the cylinder is $118 kg$ and the cross-sectional area of the cylinder is $2.29 \times 10^{- 1} m^{2}$ . The density of water is $1.03 \times 10^{3} kg m^{- 3}$ . Show that the angular frequency of oscillation of the cylinder is about $4.4 rad s^{- 1}$ .

[2]

Determine the maximum kinetic energy $E_{kmax}$ of the cylinder.

[2]

c(i).

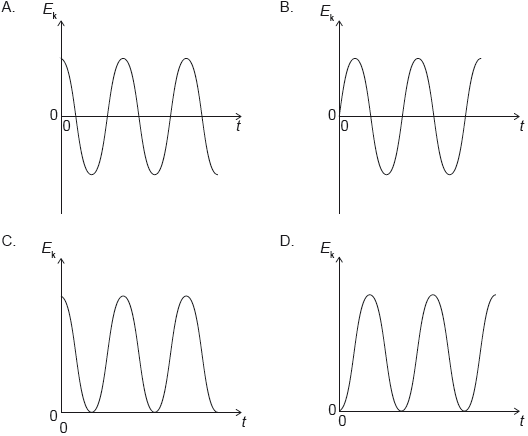
Draw, on the axes, the graph to show how the kinetic energy of the cylinder varies with time during one period of oscillation $T$ .

[2]

c(ii).

Markscheme

the «restoring» force/acceleration is proportional to displacement ✓

Allow use of symbols i.e. $F \propto - x$ or $a \propto - x$

Evidence of equating $m ω^{2} x = ρ A g x$ «to obtain $\frac{ρ A g}{m} = ω^{2}$ » ✓

$ω = \sqrt{\frac{1.03 \times 10^{3} \times 2.29 \times 10^{- 1} \times 9.81}{118}}$ OR $4.43 « rad s^{- 1} »$ ✓

Answer to at least $3$ s.f.

« $E_{K}$ is a maximum when $x = 0$ hence» $E_{K, \max} = \frac{1}{2} \times 118 \times 4 . 4^{2} (0 . 250^{2} - 0^{2})$ ✓

$71.4 « J »$ ✓

c(i).

energy never negative ✓

correct shape with two maxima ✓

c(ii).

Examiners report

This was well answered with candidates gaining credit for answers in words or symbols.

Again, very well answered.

A straightforward calculation with the most common mistake being missing the squared on the omega.

c(i).

Most candidates answered with a graph that was only positive so scored the first mark.

c(ii).

Syllabus sections

Core » Topic 4: Waves » 4.1 – Oscillations

Show 38 related questions

Hide related questions

Core » Topic 4: Waves

Core

Question

Markscheme

Examiners report

Syllabus sections

View options