IB Questionbank

User interface language: English | Español

Date	May 2022	Marks available	1	Reference code	22M.2.SL.TZ2.1
Level	Standard level	Paper	Paper 2	Time zone	2
Command term	Show that	Question number	1	Adapted from	N/A

Question

Airboats are used for transport across a river. To move the boat forward, air is propelled from the back of the boat by a fan blade.

An airboat has a fan blade of radius 1.8 m. This fan can propel air with a maximum speed relative to the boat of 20 m s⁻¹. The density of air is 1.2 kg m⁻³.

In a test the airboat is tied to the river bank with a rope normal to the bank. The fan propels the air at its maximum speed. There is no wind.

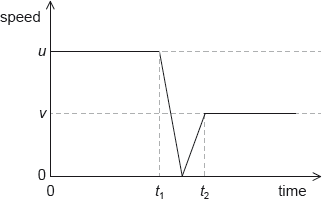
The rope is untied and the airboat moves away from the bank. The variation with time t of the speed v of the airboat is shown for the motion.

Outline why a force acts on the airboat due to the fan blade.

[3]

Show that a mass of about 240 kg of air moves through the fan every second.

[2]

b.i.

Show that the tension in the rope is about 5 kN.

[1]

b.ii.

Estimate the distance the airboat travels to reach its maximum speed.

[2]

c.i.

Deduce the mass of the airboat.

[3]

c.ii.

The fan is rotating at 120 revolutions every minute. Calculate the centripetal acceleration of the tip of a fan blade.

[2]

Markscheme

ALTERNATIVE 1

there is a force «by the fan» on the air / air is accelerated «to the rear» ✓

by Newton 3 ✓

there is an «equal and» opposite force on the boat ✓

ALTERNATIVE 2

air gains momentum «backward» ✓

by conservation of momentum / force is rate of change in momentum ✓

boat gains momentum in the opposite direction ✓

Accept a reference to Newton’s third law, e.g. N’3, or any correct statement of it for MP2 in ALT 1.

Allow any reasonable choice of object where the force of the air is acting on, e.g., fan or blades.

$π R^{2}$ OR «mass of air through system per unit time =» $A v ρ$ seen ✓

244 «kg s⁻¹» ✓

Accept use of Energy of air per second = 0.5 ρΑv³ = 0.5 mv² for MP1.

b.i.

«force = Momentum change per sec = $A v^{2} ρ$ = » 244 x 20 OR 4.9 «kN» ✓

Allow use of 240

b.ii.

recognition that area under the graph is distance covered ✓

«Distance =» 480 - 560 «m» ✓

Accept graphical evidence or calculation of correct geometric areas for MP1.

MP2 is numerical value within range.

c.i.

calculation of acceleration as gradient at t = 0 «= 1 m s^-2» ✓

use of F=ma OR $\frac{4900}{1}$ seen ✓

4900 «kg» ✓

MP1 can be shown on the graph.

Allow an acceleration in the range 1 – 1.1 for MP2 and consistent answer for MP3

Allow ECF from MP1.

Allow use of average acceleration = $\frac{18}{40}$

or assumption of constant force to obtain 11000 «kg» for [2]

Allow use of 4800 or 5000 for MP2

c.ii.

ALTERNATE 1

« ω = » 4 $π$ rad s⁻¹ ✓

« a = r ω²= » 280 « m s⁻² » ✓

ALTERNATE 2

« $v = \frac{2 π r}{T}$ » = 22.6 m s⁻¹ ✓

« $a = \frac{v^{2}}{r}$ »= 280 « m s⁻² » ✓

Allow ECF from MP1 for wrong ω (120 gives 2.6 x 10⁴« m s⁻² »)

Allow ECF from MP1 for wrong T (2 s gives 18 « m s⁻² »)

Examiners report

The majority succeeded in making use of Newton's third law to explain the force on the boat. The question was quite well answered but sequencing of answers was not always ideal. There were some confusions about the air hitting the bank and bouncing off to hit the boat. A small number thought that the wind blowing the fan caused the force on the boat.

bi) This was generally well answered with candidates either starting from the wind turbine formula given in the data booklet or with the mass of the air being found using $ρ A v$ .

1bii) Well answered by most candidates. Some creative work to end up with 240 was found in scripts.

1ci) Many candidates gained credit here for recognising that the resistive force eventually equalled the drag force and most were able to go on to link this to e.g. zero acceleration. Some had not read the question properly and assumed that the rope was still tied. There was one group of answers that stated something along the lines of "as there is no rope there is nothing to stop the boat so it can go at max speed.

1cii) A slight majority did not realise that they had to find the area under the velocity-time graph, trying equations of motion for non-linear acceleration. Those that attempted to calculate the area under the graph always succeeded in answering within the range.

1ciii) Use of the average gradient was common here for the acceleration. However, there also were answers that attempted to calculate the mass via a kinetic energy calculation that made all sorts of incorrect assumptions. Use of average acceleration taken from the gradient of the secant was also common.

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

c.i.

[N/A]

c.ii.

[N/A]