IB Questionbank

User interface language: English | Español

Date	May 2018	Marks available	1	Reference code	18M.2.HL.TZ1.1
Level	Higher level	Paper	Paper 2	Time zone	1
Command term	Describe	Question number	1	Adapted from	N/A

Question

An elastic climbing rope is tested by fixing one end of the rope to the top of a crane. The other end of the rope is connected to a block which is initially at position A. The block is released from rest. The mass of the rope is negligible.

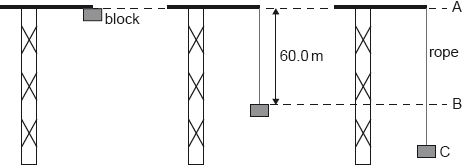
M18/4/PHYSI/SP2/ENG/TZ1/01

The unextended length of the rope is 60.0 m. From position A to position B, the block falls freely.

In another test, the block hangs in equilibrium at the end of the same elastic rope. The elastic constant of the rope is 400 Nm^–1. The block is pulled 3.50 m vertically below the equilibrium position and is then released from rest.

M18/4/PHYSI/SP2/ENG/TZ1/01

The unextended length of the rope is 60.0 m. From position A to position B, the block falls freely.

At position C the speed of the block reaches zero. The time taken for the block to fall between B and C is 0.759 s. The mass of the block is 80.0 kg.

For the rope and block, describe the energy changes that take place

At position B the rope starts to extend. Calculate the speed of the block at position B.

[2]

Determine the magnitude of the average resultant force acting on the block between B and C.

[2]

b.i.

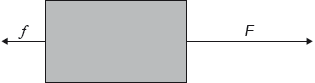
Sketch on the diagram the average resultant force acting on the block between B and C. The arrow on the diagram represents the weight of the block.

[2]

b.ii.

Calculate the magnitude of the average force exerted by the rope on the block between B and C.

[2]

b.iii.

between A and B.

[1]

c.i.

between B and C.

[1]

c.ii.

The length reached by the rope at C is 77.4 m. Suggest how energy considerations could be used to determine the elastic constant of the rope.

[2]

Calculate the time taken for the block to return to the equilibrium position for the first time.

[2]

e.i.

Calculate the speed of the block as it passes the equilibrium position.

[2]

e.ii.

Markscheme

use of conservation of energy

v² = u² + 2as

v = « $\sqrt {2 \times 60.0 \times 9.81}$ » = 34.3 «ms^–1»

[2 marks]

use of impulse F_ave × Δt = Δp

use of F = ma with average acceleration

F = $\frac{{80.0 \times 34.3}}{{0.759}}$

3620«N»

Allow ECF from (a).

[2 marks]

b.i.

upwards

clearly longer than weight

For second marking point allow ECF from (b)(i) providing line is upwards.

[2 marks]

b.ii.

3620 + 80.0 × 9.81

4400 «N»

Allow ECF from (b)(i).

[2 marks]

b.iii.

(loss in) gravitational potential energy (of block) into kinetic energy (of block)

Must see names of energy (gravitational potential energy and kinetic energy) – Allow for reasonable variations of terminology (eg energy of motion for KE).

[1 mark]

c.i.

(loss in) gravitational potential and kinetic energy of block into elastic potential energy of rope

See note for 1(c)(i) for naming convention.

Must see either the block or the rope (or both) mentioned in connection with the appropriate energies.

[1 mark]

c.ii.

k can be determined using EPE = $\frac{1}{2}$ kx²

correct statement or equation showing

GPE at A = EPE at C

(GPE + KE) at B = EPE at C

Candidate must clearly indicate the energy associated with either position A or B for MP2.

[2 marks]

T = 2π $\sqrt {\frac{{80.0}}{{400}}}$ = 2.81 «s»

time = $\frac{T}{4}$ = 0.702 «s»

Award [0] for kinematic solutions that assume a constant acceleration.

[2 marks]

e.i.

ALTERNATIVE 1

ω = $\frac{{2\pi }}{{2.81}}$ = 2.24 «rad s^–1»

v = 2.24 × 3.50 = 7.84 «ms^–1»

ALTERNATIVE 2

$\frac{1}{2}$ kx² = $\frac{1}{2}$ mv² OR $\frac{1}{2}$ 400 × 3.5² = $\frac{1}{2}$ 80v²

v = 7.84 «ms^–1»

Award [0] for kinematic solutions that assume a constant acceleration.

Allow ECF for T from (e)(i).

[2 marks]

e.ii.

Examiners report

[N/A]

b.i.

[N/A]

b.ii.

[N/A]

b.iii.

[N/A]

c.i.

[N/A]

c.ii.

[N/A]

e.i.

[N/A]

e.ii.

Syllabus sections

Core » Topic 2: Mechanics » 2.4 – Momentum and impulse

Show 69 related questions

Hide related questions

Core » Topic 2: Mechanics

Core

Question

Markscheme

Examiners report

Syllabus sections

View options