| Date | May 2017 | Marks available | 1 | Reference code | 17M.2.sl.TZ1.4 |
| Level | SL | Paper | 2 | Time zone | TZ1 |
| Command term | Deduce | Question number | 4 | Adapted from | N/A |
Question
Two hydrides of nitrogen are ammonia and hydrazine, N2H4. One derivative of ammonia is methanamine whose molecular structure is shown below.
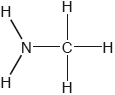
Hydrazine is used to remove oxygen from water used to generate steam or hot water.
N2H4(aq) + O2(aq) → N2(g) + 2H2O(l)
The concentration of dissolved oxygen in a sample of water is 8.0 × 10−3 gdm−3.
Estimate the H−N−H bond angle in methanamine using VSEPR theory.
Ammonia reacts reversibly with water.
NH3(g) + H2O(l) NH4+(aq) + OH−(aq)
Explain the effect of adding H+(aq) ions on the position of the equilibrium.
Hydrazine reacts with water in a similar way to ammonia. Deduce an equation for the reaction of hydrazine with water.
Outline, using an ionic equation, what is observed when magnesium powder is added to a solution of ammonium chloride.
Hydrazine has been used as a rocket fuel. The propulsion reaction occurs in several stages but the overall reaction is:
N2H4(l) → N2(g) + 2H2(g)
Suggest why this fuel is suitable for use at high altitudes.
Determine the enthalpy change of reaction, ΔH, in kJ, when 1.00 mol of gaseous hydrazine decomposes to its elements. Use bond enthalpy values in section 11 of the data booklet.
N2H4(g) → N2(g) + 2H2(g)
The standard enthalpy of formation of N2H4(l) is +50.6 kJmol−1. Calculate the enthalpy of vaporization, ΔHvap, of hydrazine in kJmol−1.
N2H4(l) → N2H4(g)
(If you did not get an answer to (f), use −85 kJ but this is not the correct answer.)
Calculate, showing your working, the mass of hydrazine needed to remove all the dissolved oxygen from 1000 dm3 of the sample.
Calculate the volume, in dm3, of nitrogen formed under SATP conditions. (The volume of 1 mol of gas = 24.8 dm3 at SATP.)
Markscheme
107°
Accept 100° to < 109.5°.
Literature value = 105.8°
[1 mark]
removes/reacts with OH−
moves to the right/products «to replace OH− ions»
Accept ionic equation for M1.
[2 marks]
N2H4(aq) + H2O(l) N2H5+(aq) + OH–(aq)
Accept N2H4(aq) + 2H2O(l) N2H62+(aq) + 2OH–(aq).
Equilibrium sign must be present.
[1 mark]
bubbles
OR
gas
OR
magnesium disappears
2NH4+(aq) + Mg(s) → Mg2+(aq) + 2NH3(aq) + H2(g)
Do not accept “hydrogen” without reference to observed changes.
Accept "smell of ammonia".
Accept 2H+(aq) + Mg(s) → Mg2+(aq) + H2(g)
Equation must be ionic.
[2 mark]
no oxygen required
[1 mark]
bonds broken:
E(N–N) + 4E(N–H)
OR
158 «kJmol–1» + 4 x 391 «kJmol–1» / 1722 «kJ»
bonds formed:
E(N≡N) + 2E(H–H)
OR
945 «kJmol–1» + 2 x 436 «kJmol–1» / 1817 «kJ»
«ΔH = bonds broken – bonds formed = 1722 – 1817 =» –95 «kJ»
Award [3] for correct final answer.
Award [2 max] for +95 «kJ».
[3 marks]
OR
ΔHvap= −50.6 kJmol−1 − (−95 kJmol−1)
«ΔHvap =» +44 «kJmol−1»
Award [2] for correct final answer.
Award [1 max] for −44 «kJmol−1».
Award [2] for:
ΔHvap − = 50.6 kJmol−1 − (−85 kJmol−1) + = 34 «kJmol−1».
Award [1 max] for −34 «kJmol−1».
[2 marks]
total mass of oxygen «= 8.0 x 10–3 gdm–3 x 1000 dm3» = 8.0 «g»
n(O2) «» 0.25 «mol»
OR
n(N2H4) = n(O2)
«mass of hydrazine = 0.25 mol x 32.06 gmol–1 =» 8.0 «g»
Award [3] for correct final answer.
[3 marks]
«n(N2H4) = n(O2) » 0.25 «mol»
«volume of nitrogen = 0.25 mol x 24.8 dm3mol–1» = 6.2 «dm3»
Award [1] for correct final answer.
[1 mark]

