| Date | May 2015 | Marks available | 2 | Reference code | 15M.3dm.hl.TZ0.4 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Draw | Question number | 4 | Adapted from | N/A |
Question
A simple connected planar graph, has \(e\) edges, \(v\) vertices and \(f\) faces.
(i) Show that \(2e \ge 3f{\text{ if }}v > 2\).
(ii) Hence show that \({K_5}\), the complete graph on five vertices, is not planar.
(i) State the handshaking lemma.
(ii) Determine the value of \(f\), if each vertex has degree \(2\).
Draw an example of a simple connected planar graph on \(6\) vertices each of degree \(3\).
Markscheme
(i) METHOD 1
attempting to use \(f = e - v + 2\) and \(e \le 3v - 6\) (if \(v > 2\)) (M1)
\(2e \le 6v - 12 = 6(e - f + 2) - 12\) M1A1
leading to \(2e \ge 3f\) AG
METHOD 2
each face is bounded by at least three edges A1
Note: Award A1 for stating \(e \ge 3f\).
each edge either separates two faces or, if an edge is interior to a face, it gets counted twice R1
Note: Award R1 for stating that each edge contributes two to the sum of the degrees of the faces (or equivalent) ie, \(\sum {\deg (F) = 2e} \).
adding up the edges around each face R1
leading to \(2e \ge 3f\) AG
(ii) \({K_5}\) has \(e = 10\) A1
if the graph is planar, \(f = 7\) A1
this contradicts the inequality obtained above R1
hence the graph is non-planar AG
[6 marks]
(i) the sum of the vertex degrees \( = 2e\) (or is even) or equivalent A1
(ii) if each vertex has degree \(2\), then \(2v = 2e\) A1
substituting \(v = e\) into Euler’s formula M1
\(f = 2\) A1
[4 marks]
for example,
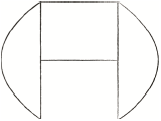 A2
A2
[2 marks]
Total [12 marks]
Examiners report
In part (a) (i), many candidates tried to prove \(2e \ge 3f\) with numerical examples. Only a few candidates were able to prove this inequality correctly. In part (a) (ii), most candidates knew that \({K_5}\) has 10 edges. However, a number of candidates simply drew a diagram with any number of faces and used this particular representation as a basis for their 'proof'. Many candidates did not recognise the 'hence' requirement in part (a) (ii).
In part (b) (i), many candidates stated the 'handshaking lemma' incorrectly by relating it to the 'handshake problem'. In part (b) (ii), only a few candidates determined that \(v = e\) and hence found that \(f = 2\).
In part (c), a reasonable number of candidates were able to draw a simple connected planar graph on \(6\) vertices each of degree \(3\). The most common error here was to produce a graph that contained a multiple edge(s).

