| Date | May 2015 | Marks available | 2 | Reference code | 15M.3dm.hl.TZ0.2 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Draw | Question number | 2 | Adapted from | N/A |
Question
The graph \({K_{2,{\text{ }}2}}\) is the complete bipartite graph whose vertex set is the disjoint union of two subsets each of order two.
Draw \({K_{2,{\text{ }}2}}\) as a planar graph.
Draw a spanning tree for \({K_{2,{\text{ }}2}}\).
Draw the graph of the complement of \({K_{2,{\text{ }}2}}\).
Show that the complement of any complete bipartite graph does not possess a spanning tree.
Markscheme
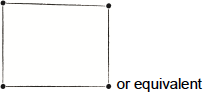 A1A1
A1A1
Note: Award A1 for a correct version of \({K_{2,{\text{ }}2}}\) and A1 for a correct planar representation.
[2 marks]
 A1
A1
[1 mark]
 A1
A1
[1 mark]
the complete bipartite graph \({K_{m,{\text{ }}n}}\) has two subsets of vertices \(A\) and \(B\), such that each element of \(A\) is connected to every element of \(B\) A1
in the complement, no element of \(A\) is connected to any element of \(B\). The complement is not a connected graph A1
by definition a tree is connected R1
hence the complement of any complete bipartite graph does not possess a spanning tree AG
[3 marks]
Total [7 marks]
Examiners report
Part (a) was generally well done with a large number of candidates drawing a correct planar representation for \({K_{2,2}}\). Some candidates, however, produced a correct non-planar representation of \({K_{2,2}}\).
Parts (b) and (c) were generally well done with many candidates drawing a correct spanning tree for \({K_{2,2}}\) and the correct complement of \({K_{2,2}}\).
Parts (b) and (c) were generally well done with many candidates drawing a correct spanning tree for \({K_{2,2}}\) and the correct complement of \({K_{2,2}}\).
Part (d) tested a candidate’s ability to produce a reasoned argument that clearly explained why the complement of \({K_{m,n}}\) does not possess a spanning tree. This was a question part in which only the best candidates provided the necessary rigour in explanation.

