| Date | May 2017 | Marks available | 2 | Reference code | 17M.3dm.hl.TZ0.1 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Hence and Find | Question number | 1 | Adapted from | N/A |
Question
Use the Euclidean algorithm to find the greatest common divisor of 264 and 1365.
Hence, or otherwise, find the general solution of the Diophantine equation
\[264x - 1365y = 3.\]
Hence find the general solution of the Diophantine equation
\[264x - 1365y = 6.\]
By expressing each of 264 and 1365 as a product of its prime factors, determine the lowest common multiple of 264 and 1365.
Markscheme
\(1365 = 5 \times 264 + 45\) M1
\(264 = 5 \times 45 + 39\) A1
\(45 = 1 \times 39 + 6\) A1
\(39 = 6 \times 6 + 3\)
\(6 = 2 \times 3\) A1
so gcd is 3
[5 marks]
EITHER
\(39 - 6 \times 6 = 3\) (M1)
\(39 - 6 \times (45 - 39) = 3 \Rightarrow 7 \times 39 - 6 \times 45 = 3\) (A1)
\(7 \times (264 - 5 \times 45) - 6 \times 45 = 3 \Rightarrow 7 \times 264 - 41 \times 45 = 3\) (A1)
\(7 \times 264 - 41 \times (1365 - 5 \times 264) = 3 \Rightarrow 212 \times 264 - 41 \times 1365 = 3\) (A1)
OR
tracking the linear combinations when applying the Euclidean algorithm (could be displayed in (a))
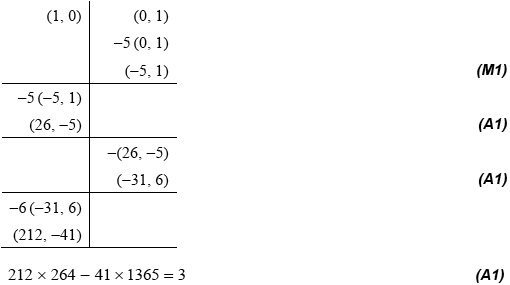
THEN
a solution is \(x = 212,y = 41\) (or equivalent eg \(x = - 243,y = - 47\)) (A1)
\(x = 212 + 455N,y = 41 + 88N\) (or equivalent) \((N \in \mathbb{Z})\) A1
[6 marks]
a solution is \(x = 424,y = 82{\text{ }}({\text{or equivalent }}eg{\text{ }}x = - 31,{\text{ }}y = - 6)\) (A1)
\(x = 424 + 455N,{\text{ }}y = 82 + 88N({\text{or equivalent}}){\text{ }}\left( {N \in \mathbb{Z}} \right)\) A1
Note: Award A1A0 for \(x = 424 + 910N,{\text{ }}y = 82 + 176N\).
[2 marks]
\(264 = 2 \times 2 \times 2 \times 3 \times 11\) A1
\(1365 = 3 \times 5 \times 7 \times 13\) A1
\(1\,{\text{cm}} = 2 \times 2 \times 2 \times 3 \times 5 \times 7 \times 11 \times 13 = 120120\) A1
Note: Only award marks if prime factorisation is used.
[3 marks]

