| Date | November 2016 | Marks available | 6 | Reference code | 16N.3ca.hl.TZ0.3 |
| Level | HL only | Paper | Paper 3 Calculus | Time zone | TZ0 |
| Command term | Determine | Question number | 3 | Adapted from | N/A |
Question
Consider the infinite spiral of right angle triangles as shown in the following diagram.
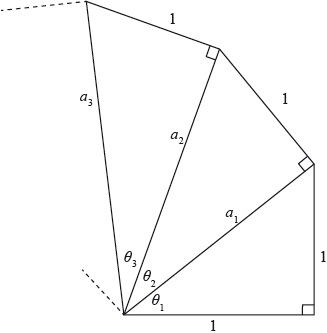
The \(n{\text{th}}\) triangle in the spiral has central angle \({\theta _n}\), hypotenuse of length \({a_n}\) and opposite side of length 1, as shown in the diagram. The first right angle triangle is isosceles with the two equal sides being of length 1.
Consider the series \(\sum\limits_{n = 1}^\infty {{\theta _n}} \).
Using l’Hôpital’s rule, find \(\mathop {\lim }\limits_{x \to \infty } \left( {\frac{{\arcsin \left( {\frac{1}{{\sqrt {(x + 1)} }}} \right)}}{{\frac{1}{{\sqrt x }}}}} \right)\).
(i) Find \({a_1}\) and \({a_2}\) and hence write down an expression for \({a_n}\).
(ii) Show that \({\theta _n} = \arcsin \frac{1}{{\sqrt {(n + 1)} }}\).
Using a suitable test, determine whether this series converges or diverges.
Markscheme
\(\mathop {\lim }\limits_{x \to \infty } \left( {\frac{{\arcsin \left( {\frac{1}{{\sqrt {(x + 1)} }}} \right)}}{{\frac{1}{{\sqrt x }}}}} \right)\) is of the form \(\frac{0}{0}\)
and so will equal the limit of \(\frac{{\frac{{\frac{{ - 1}}{2}{{(x + 1)}^{ - \frac{3}{2}}}}}{{\sqrt {1 - \left( {\frac{1}{{x + 1}}} \right)} }}}}{{\frac{{ - 1}}{2}{x^{ - \frac{3}{2}}}}}\) M1M1A1A1
Note: M1 for attempting differentiation of the top and bottom, M1A1 for derivative of top (only award M1 if chain rule is used), A1 for derivative of bottom.
\( = \mathop {\lim }\limits_{x \to \infty } \frac{{{{\left( {\frac{x}{{(x + 1)}}} \right)}^{\frac{3}{2}}}}}{{\sqrt {\frac{x}{{x + 1}}} }} = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{x}{{x + 1}}} \right)\) M1
Note: Accept any intermediate tidying up of correct derivative for the method mark.
\( = 1\) A1
[6 marks]
(i) \({a_1} = \sqrt 2 ,{\text{ }}{a_2} = \sqrt 3 \) A1
\({a_n} = \sqrt {n + 1} \) A1
(ii) \(\sin {\theta _n} = \frac{1}{{{a_n}}} = \frac{1}{{\sqrt {n + 1} }}\) A1
Note: Allow \({\theta _n} = \arcsin \left( {\frac{1}{{{a_n}}}} \right)\) if \({a_n} = \sqrt {n + 1} \) in b(i).
so \({\theta _n} = \arcsin \frac{1}{{\sqrt {(n + 1)} }}\) AG
[3 marks]
for \(\sum\limits_{n = 1}^\infty {\arcsin \frac{1}{{\sqrt {(n + 1)} }}} \) apply the limit comparison test (since both series of positive terms) M1
with \(\sum\limits_{n = 1}^\infty {\frac{1}{{\sqrt n }}} \) A1
from (a) \(\mathop {\lim }\limits_{n \to \infty } \frac{{\arcsin \frac{1}{{\sqrt {(n + 1)} }}}}{{\frac{1}{{\sqrt n }}}} = 1\), so the two series either both converge or both diverge M1R1
\(\sum\limits_{n = 1}^\infty {\frac{1}{{\sqrt 2 }}} \) diverges (as is a \(p\)-series with \(p = \frac{1}{2}\)) A1
hence \(\sum\limits_{n = 1}^\infty {{\theta _n}} \) diverges A1
[6 marks]

