| Date | May 2016 | Marks available | 10 | Reference code | 16M.1.hl.TZ2.12 |
| Level | HL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find and Show that | Question number | 12 | Adapted from | N/A |
Question
Let \(w = \cos \frac{{2\pi }}{7} + {\text{i}}\sin \frac{{2\pi }}{7}\).
Consider the quadratic equation \({z^2} + bz + c = 0\) where \(b,{\text{ }}c \in \mathbb{R},{\text{ }}z \in \mathbb{C}\). The roots of this equation are \(\alpha \) and \(\alpha *\) where \(\alpha *\) is the complex conjugate of \(\alpha \).
Verify that \(w\) is a root of the equation \({z^7} - 1 = 0,{\text{ }}z \in \mathbb{C}\).
(i) Expand \((w - 1)(1 + w + {w^2} + {w^3} + {w^4} + {w^5} + {w^6})\).
(ii) Hence deduce that \(1 + w + {w^2} + {w^3} + {w^4} + {w^5} + {w^6} = 0\).
Write down the roots of the equation \({z^7} - 1 = 0,{\text{ }}z \in \mathbb{C}\) in terms of \(w\) and plot these roots on an Argand diagram.
(i) Given that \(\alpha = w + {w^2} + {w^4}\), show that \(\alpha * = {w^6} + {w^5} + {w^3}\).
(ii) Find the value of \(b\) and the value of \(c\).
Using the values for \(b\) and \(c\) obtained in part (d)(ii), find the imaginary part of \(\alpha \), giving your answer in surd form.
Markscheme
EITHER
\({w^7} = {\left( {\cos \frac{{2\pi }}{7} + {\text{i}}\sin \frac{{2\pi }}{7}} \right)^7}\) (M1)
\( = \cos 2\pi + {\text{i}}\sin 2\pi \) A1
\( = 1\) A1
so \(w\) is a root AG
OR
\({z^7} = 1 = \cos (2\pi k) + {\text{i}}\sin (2\pi k)\) (M1)
\(z = \cos \left( {\frac{{2\pi k}}{7}} \right) + {\text{i}}\sin \left( {\frac{{2\pi }}{7}} \right)\) A1
\(k = 1 \Rightarrow z = \cos \left( {\frac{{2\pi }}{7}} \right) + {\text{i}}\sin \left( {\frac{{2\pi }}{7}} \right)\) A1
so \(w\) is a root AG
[3 marks]
(i) \((w - 1)(1 + w + {w^2} + {w^3} + {w^4} + {w^5} + {w^6})\)
\( = w + {w^2} + {w^3} + {w^4} + {w^5} + {w^6} + {w^7} - 1 - w - {w^2} - {w^3} - {w^4} - {w^5} - {w^6}\) M1
\( = {w^7} - 1{\text{ }}( = 0)\) A1
(ii) \({w^7} - 1 = 0\) and \(w - 1 \ne 0\) R1
so \(1 + w + {w^2} + {w^3} + {w^4} + {w^5} + {w^6} = 0\) AG
[3 marks]
the roots are \(1,{\text{ }}w,{\text{ }}{w^2},{\text{ }}{w^3},{\text{ }}{w^4},{\text{ }}{w^5}\) and \({w^6}\)
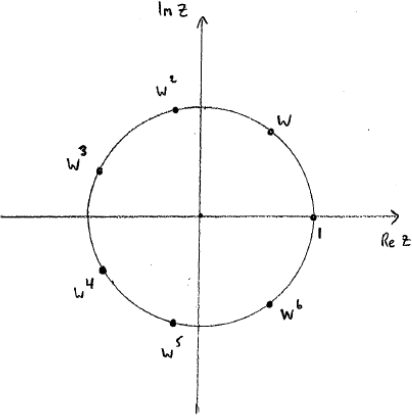
7 points equidistant from the origin A1
approximately correct angular positions for \(1,{\text{ }}w,{\text{ }}{w^2},{\text{ }}{w^3},{\text{ }}{w^4},{\text{ }}{w^5}\) and \({w^6}\) A1
Note: Condone use of cis notation for the final two A marks.
Note: For the final A mark there should be one root in the first quadrant, two in the second, two in the third, one in the fourth, and one on the real axis.
[3 marks]
(i) \(\alpha * = (w + {w^2} + {w^4})*\)
\( = w* + ({w^2})* + ({w^4})*\) A1
since \( = w* = {w^6},{\text{ }}({w^2})* = {w^5}\) and \(({w^4})* = {w^3}\) R1
\( \Rightarrow \alpha * = {w^6} + {w^5} + {w^3}\) AG
(ii) \(b = - (\alpha + \alpha *)\) (using sum of roots (or otherwise)) (M1)
\(b = - (w + {w^2} + {w^3} + {w^4} + {w^5} + {w^6})\) (A1)
\( = - ( - 1)\)
\( = 1\) A1
\(c = \alpha \alpha *\) (using product of roots (or otherwise)) (M1)
\(c = (w + {w^2} + {w^4})({w^6} + {w^5} + {w^3})\)
EITHER
\( = {w^{10}} + {w^9} + {w^8} + 3{w^7} + {w^6} + {w^5} + {w^4}\) A1
\( = ({w^6} + {w^5} + {w^4} + {w^3} + {w^2} + w) + 3\) M1
\( = 3 - 1\) (A1)
OR
\( = {w^{10}} + {w^9} + {w^8} + 3{w^7} + {w^6} + {w^5} + {w^4}\left( { = {w^4}(1 + w + {w^3})({w^3} + {w^2} + 1)} \right)\) A1
\( = {w^4}({w^6} + {w^5} + {w^4} + {w^2} + w + 1 + 3{w^3})\) M1
\( = {w^4}({w^6} + {w^5} + {w^4} + {w^3} + {w^2} + w + 1 + 2{w^3})\)
\( = {w^4}(2{w^3})\) (A1)
THEN
\( = 2\) A1
[10 marks]
\({z^2} + z + 2 = 0 \Rightarrow z = \frac{{ - 1 \pm {\text{i}}\sqrt 7 }}{2}\) M1A1
\(\operatorname{Im} (w + {w^2} + {w^4}) > 0\) R1
\(\operatorname{Im} \alpha = \frac{{\sqrt 7 }}{2}\) A1
Note: Final A mark is independent of previous R mark.
[4 marks]
Examiners report
The majority of candidates scored full marks in part (a).
The majority of candidates scored full marks in part (b)(i). It was expected to see \(w - 1 \ne 0\) stated for the (b)(ii) mark, though some did appreciate this.
In part (c), the roots were required to be stated in terms of \(w\). This was sometimes ignored, thankfully not too frequently. Clear Argand diagrams were not often seen, and candidates’ general presentation in this area could be improved. Having said this, most scripts were awarded at least 2 of 3 marks available.
Part (d) proved to be a good discriminator for the better candidates. The product and sum of roots formulae now seem to be better appreciated, and while only the best scored full marks, a good number were able to demonstrate the result \(b = 1\).
In part (e), of those candidates who reached this far in the paper, most were able to pick up two or three marks, albeit from sometimes following through incorrect work. A correct reason for choosing \({\text{i}}\sqrt 7 \) over \( - {\text{i}}\sqrt 7 \) was necessary, but rarely, if ever seen.

