| Date | May 2014 | Marks available | 3 | Reference code | 14M.3.SL.TZ2.18 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Determine and State | Question number | 18 | Adapted from | N/A |
Question
This question is about a magnifying glass and a telescope.
A thin converging (convex) lens is used as a magnifying glass. Object O is placed between a focal point of the lens and the centre of the lens. The focal points of the lens are shown, labelled F.
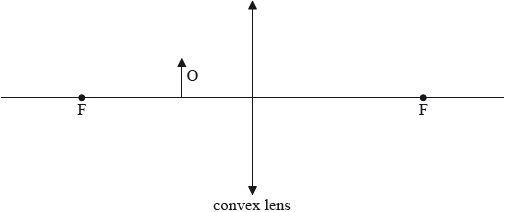
The position of the lens in (a) is changed so that a virtual image of the object is formed at the near point of the eye. The eye is very close to the lens.
The lens in (a) has a focal length of 6.0 cm and is now used as the eyepiece of an astronomical telescope. The objective lens of the telescope has a focal length of 90 cm. The telescope is used in normal adjustment.
(i) Define the term focal point.
(ii) On the diagram, construct rays to locate the position of the image of the object. Label the image I.
(i) Define the term near point.
(ii) Outline the advantage of having the image positioned at the near point of the eye.
(i) State the separation of the objective lens and the eyepiece lens.
(ii) Determine the angular magnification of the telescope.
Markscheme
(i) the point on the principal axis;
through which rays parallel to the principal axis pass after going through the lens / from which rays are parallel to the principal axis after passing through the lens;
Allow marking points on a labelled diagram.
(ii) 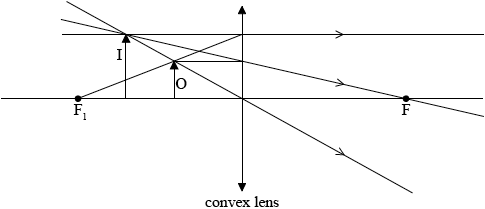
any correct ray of the three shown in the diagram;
second ray correct;
image shown correctly, between O and \({{\text{F}}_{\text{1}}}\);
Accept rays without arrows and solid construction lines back to the image.
(i) closest point on which the eye can focus (comfortably); } (allow closest distance)
(ii) gives maximum angular magnification (without straining the eye);
(i) separation = 96 (cm);
(ii) \(M = \left( {\frac{{{f_{\text{o}}}}}{{{f_{\text{e}}}}} = } \right){\text{ }}\frac{{90}}{{6.0}}\);
\(M = 15\);

