| Date | November 2010 | Marks available | 2 | Reference code | 10N.3.SL.TZ0.G2 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | State | Question number | G2 | Adapted from | N/A |
Question
This question is about an astronomical telescope.
The diagram (not to scale) shows the arrangement of the two convex lenses in an astronomical telescope in normal adjustment.
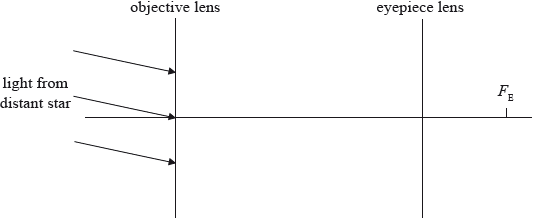
The telescope is used to observe a distant star. One of the focal points of the eyepiece lens is labelled \({F_{\text{E}}}\).
On the diagram above,
(i) label, with the symbol \({F_{\text{E}}}\), the position of the other focal point of the eyepiece lens.
(ii) label, with the symbol \({F_{\text{O}}}\), the position of the focal point of the objective lens that is in between the two lenses.
(iii) construct rays to locate the final image of the star.
In a particular astronomical telescope, the eyepiece lens has a power of 40 dioptres and the objective lens a power of 0.80 dioptres. Determine the angular magnification of the telescope in normal adjustment.
In an astronomical telescope the objective is often made up from a diverging and a converging lens, whereas the aperture of the eyepiece is usually restricted such that only rays close to the principal axis are viewed. State the reasons for this.
Objective lens:
Eyepiece lens:
Markscheme
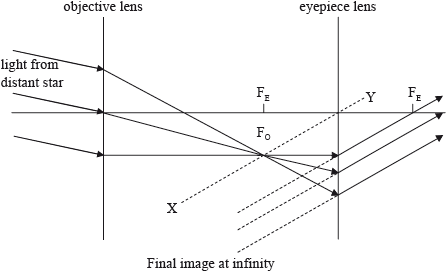
(i) same distance to left of eyepiece as \({{\text{F}}_{\text{E}}}\) is to the right; (judge by eye)
(ii) coincident with \({{\text{F}}_{\text{E}}}\) as labelled in (a)(i);
(iii) three rays meeting at focal plane of the two lenses;
construction line XY;
rays refracted at eyepiece;
extrapolation to indicate final image at infinity with label;
Do not penalize if rays do not have arrows.
\({f_{\text{e}}} = \left( {\frac{1}{{40}} = } \right){\text{ }}2.5{\text{ cm and }}{f_{\text{o}}} = \left( {\frac{1}{{0.80}} = } \right){\text{ }}125{\text{ cm}}\);
\(M = \left( {\frac{{{f_{\text{o}}}}}{{{f_{\text{e}}}}} = } \right){\text{ }}\left( {\frac{{125}}{{2.5}} = } \right){\text{ }}50\);
objective lens: to eliminate/minimize chromatic aberration;
eyepiece lens: to eliminate/minimize spherical aberration;
Examiners report
In part (a), as in past papers, ray diagrams were often poor. Many candidates failed to identify the correct locations of the two focal points.
Candidates who recognised that the power of a lens is the reciprocal of its focal length had little difficulty with the problem on angular magnification.
Most candidates were aware of chromatic and spherical aberration.

