| Date | May 2014 | Marks available | 4 | Reference code | 14M.2.SL.TZ2.5 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Determine and Identify | Question number | 5 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about simple harmonic motion (SHM) and sound. Part 2 is about electric and magnetic fields.
Part 1 Simple harmonic motion (SHM) and sound
The diagram shows a section of continuous track of a long-playing (LP) record. The stylus (needle) is placed in the track of the record.
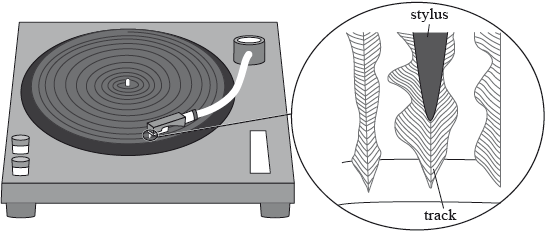
As the LP record rotates, the stylus moves because of changes in the width and position of the track. These movements are converted into sound waves by an electrical system and a loudspeaker.
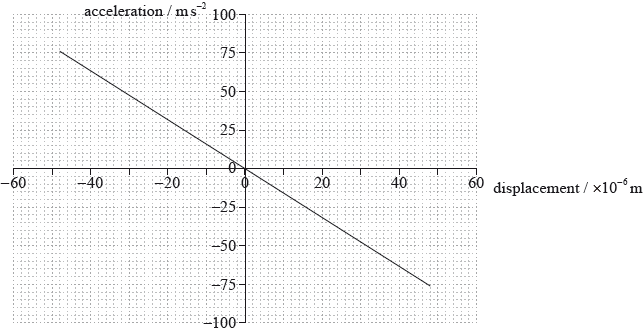
A recording of a single-frequency musical note is played. The graph shows the variation in horizontal acceleration of the stylus with horizontal displacement.
Sound is emitted from a loudspeaker which is outside a building. The loudspeaker emits a sound wave that has the same frequency as the recorded note.
A person standing at position 1 outside the building and a person standing at position 2 inside the building both hear the sound emitted by the loudspeaker.
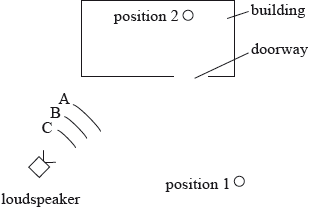
A, B and C are wavefronts emitted by the loudspeaker.
Part 2 Electric and magnetic fields
Electrical leads used in physics laboratories consist of a central conductor surrounded by an insulator.
Explain why the graph shows that the stylus undergoes simple harmonic motion.
(i) Using the graph on page 14, show that the frequency of the note being played is about 200 Hz.
(ii) On the graph on page 14, identify, with the letter P, the position of the stylus at which the kinetic energy is at a maximum.
(i) Draw rays to show how the person at position 1 is able to hear the sound emitted by the loudspeaker.
(ii) The speed of sound in the air is \({\text{330 m}}\,{{\text{s}}^{ - 1}}\). Calculate the wavelength of the note.
(iii) The walls of the room are designed to absorb sound. Explain how the person at position 2 is able to hear the sound emitted by the loudspeaker.
The arrangement in (c) is changed and another loudspeaker is added. Both loudspeakers emit the same recorded note in phase with each other.
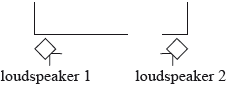
Outline why there are positions between the loudspeakers where the sound can only be heard faintly.
Distinguish between an insulator and a conductor.
The diagram shows a current I in a vertical wire that passes through a hole in a horizontal piece of cardboard.
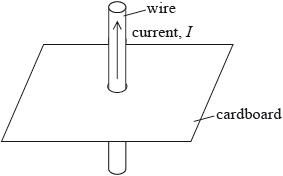
On the cardboard, draw the magnetic field pattern due to the current.
(i) The diagram shows a length of copper wire that is horizontal in the magnetic field of the Earth.
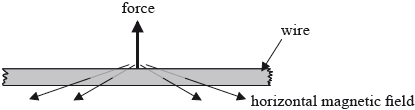
The wire carries an electric current and the force on the wire is as shown. Identify, with an arrow, the direction of electron flow in the wire.
(ii) The horizontal component of the magnetic field of the Earth at the position of the wire is \({\text{40 }}\mu {\text{T}}\). The mass per unit length of the wire is \({\text{1.41}} \times {\text{1}}{{\text{0}}^{ - 4}}{\text{ kg}}\,{{\text{m}}^{ - 2}}\). The net force on the wire is zero. Determine the current in the wire.
Markscheme
acceleration is proportional to displacement;
force/acceleration is directed towards equilibrium (point)/rest position; } (do not accept “centre” or “fixed” point)
straight line through the origin shows the proportionality;
negative gradient shows acceleration directed towards equilibrium (point) / acceleration has opposite sign to displacement;
(i) gradient \( = ( - ){\omega ^2}\);
\({\omega ^2} = 1.56 \times {10^6}{\text{ (}}{{\text{s}}^{ - 2}}{\text{)}}\);
\(\omega = 1250{\text{ (rad}}\,{{\text{s}}^{ - 1}}{\text{)}}\);
\(f = 198{\text{ (Hz)}}\);
or
\({\omega ^2} = ( - )\frac{a}{x}\);
\(\omega = \sqrt {\frac{{75}}{{48 \times {{10}^{ - 6}}}}} \);
\(f = \frac{1}{{2\pi }}\sqrt {\frac{{75}}{{48 \times {{10}^{ - 6}}}}} \);
\(f = 198{\text{ (Hz)}}\);
Allow substitution for fourth mark.
(ii) at origin;
(i) ray shown at 90° to wavefront A, plausible reflection and reflected ray goes in direction of position 1; } (judge by eye)
(ii) 1.65 (m); (allow ECF from (b)) (accept rounding to 1.6 or 1.7)
(iii) mention of diffraction;
diffraction means that sound spreads beyond the limit of geometrical shadow/can go around a corner / OWTTE;
Accept marking points in the form of a clearly drawn correctly labelled diagram.
interference/superposition mentioned;
when sounds arrive out of phase / path difference half integer number of wavelengths / OWTTE;
cancellation occurs / destructive (interference);
some (back) reflection from walls so cancellation may not be complete (hence “faint” not “zero”);
conductor has free electrons/charges that are free to move within/through it / insulator does not have free electrons/charges that are free to move within/ through it;
electrons act as charge carriers;
when a pd acts across a conductor a current exists when charge (carriers) move;
Do not allow “good/bad conductor/resistor” or reference to conductivity/resistivity.
anti-clockwise arrows;
at least three circles centred on wire;
increasing in separation from centre;
(i) arrow to the right;
(ii) \(\frac{F}{l} = BI\);
\(I = \left( {\frac{{mg}}{{lB}} = } \right)\frac{{1.41 \times {{10}^{ - 4}} \times 9.8}}{{40 \times {{10}^{ - 6}}}}\);
35 (A);
Award [3] for a bald correct answer.
Allow use of g = 10 m\(\,\)s–2 which also gives an answer of 35 (A).
Examiners report
It was rare to see all four marks awarded for statements of the requirements of harmonic oscillation and recognition of these in the straight-line graph. Candidates were generally happy to state that acceleration is directly proportional to displacement and that the straight line through the origin confirmed this. Correct statements with appropriate detail of the direction of the force/acceleration were rarer and the negative gradient was not often mentioned. Four marks were available and therefore candidates should have recognised that four points were required.
(i) This calculation was poorly done.
(ii) P – when it was marked on the graph at all – was either shown at the origin (correct) or one extreme (incorrect) of the graph in about equal numbers.
(i) Candidates are required to know the relationship between wavefronts and rays and it was surprising that many completed the diagram with wavefronts – and even these would not have gained much credit given the very poor draughtsmanship in evidence. Few candidates bothered to read the question. They failed to realise that all they were required to do was construct plausible incident and reflected rays that would enable the observer at point 1 to hear the sound.
(ii) There were many examples of correct evaluation of the wavelength of the sound but far too many were unable to complete this simple task. Inversions of the equation and mistakes in powers of ten and in rounding were common.
(iii) The usual phonetic spelling of “defraction” was observed. Examiners are unlikely to give a benefit of the doubt to what might have been a phonetic spelling or might equally have been confusion with “refraction” in this particular case. Many candidates were able to spot that the sound was being diffracted but an explanation of what diffraction is, in context, was much rarer.
Superficial answers were common. Candidates continue to ignore the mark allocations for questions and therefore the number of independent points they should mention in an answer. Here, most said that conductors contain free electrons (or the reverse for insulators) but did not go on to discuss the role of the free electrons in carrying charge or to relate the current to the existence of an electric field across the conductor. Far too many gave answers of the “conductors conduct well” variety that do not score marks.
There are three elements to a good drawing of the magnetic field around a long straight conductor: the concentric circularity of the lines, the direction of the lines related to the direction of charge flow, and the increasing separation between lines as the distance from the conductor increases. It was a rare candidate who was able to convince the examiner with all three points. In hindsight, the diagram could have been larger on the page. However, candidates could have taken more trouble over their sketches which were usually crude.
(i) Many forgot that the sign rules involve conventional current and lost the mark.
(ii) Few correct solutions were observed. This was a straightforward problem involving one re-arrangement of a standard equation and the incorporation of the weight of the conductor.

