| Date | May 2014 | Marks available | 3 | Reference code | 14M.3.HL.TZ2.14 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Determine | Question number | 14 | Adapted from | N/A |
Question
This question is about thin-film interference.
A thin layer of oil of refractive index 1.51 floats on water of refractive index 1.33. Light of wavelength 579 nm is incident normally to the surface.
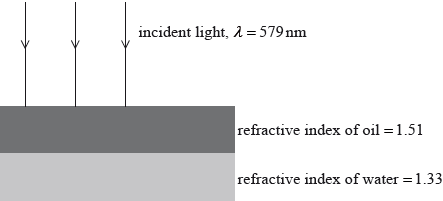
Determine the minimum thickness of the oil layer that gives rise to the least amount of light being reflected.
Describe the change in the intensity of the reflected light as the thickness of the oil layer in (a) is gradually increased.
Markscheme
use of \(m = 1\);
\(2 \times 1.51 \times t = 1 \times 579 \times {10^{ - 9}}\);
\(t = 1.92 \times {10^{ - 7}}{\text{ (m)}}\);
Award [3] for a bald correct answer.
Award [2 max] for use of \(m = \frac{1}{2}\) giving 9.6 \( \times \) 10–8 (m).
Award [2 max] for answer of \(\frac{\lambda }{2}\) for air (2.9 \( \times \) 10–7 (m)).
intensity increases;
intensity then decreases and increases repeatedly;
when thickness becomes very large the intensity becomes constant;
Examiners report
In (a) the correct thin film formula from the data booklet was sometimes chosen, but many candidates were able to answer the question using first principles. A common mistake was was to give the half wavelength value in air rather than oil or to forget the phase change on the hard reflection.
Few could give a well reasoned answer to (b) and were often lucky to score one mark.

