| Date | November 2010 | Marks available | 1 | Reference code | 10N.3.HL.TZ0.G5 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | State | Question number | G5 | Adapted from | N/A |
Question
This question is about thin-film interference.
The diagram (not to scale) represents an experimental set-up designed to measure the diameter of a human hair.
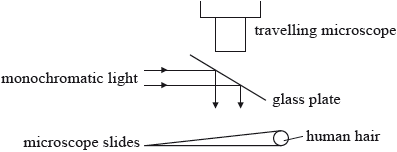
A hair is used to separate two microscope slides. A monochromatic beam of light is reflected onto the two slides by the glass plate. The light is then reflected from the two slides and transmitted through the glass plate and is viewed by the travelling microscope.
State why the light reflected from the two microscope slides produces a system of interference fringes.
The condition that a bright fringe is observed in the field of view of the travelling microscope is given by the relationship
\[2t = \left( {m + \frac{1}{2}} \right)\lambda \]
where \(t\) is the thickness of the air film formed by the wedge at the point where the bright fringe is observed, \(m\) is an integer and \(\lambda \) is the wavelength of the incident light.
State the reason for the factor \(\frac{1}{2}\) in the relationship.
In the diagram, the length of the slides is 5.00 cm. The wavelength of the monochromatic light is \(5.92 \times {10^{ - 7}}{\text{ m}}\). Using the travelling microscope it is observed that 50 fringes occupy a length of 0.940 cm. Show that the diameter of the hair used to separate the slides is about \({\text{80 }}\mu {\text{m}}\).
Markscheme
light reflected from the top slide interferes with light reflected from the bottom slide;
the light reflected from the bottom slide undergoes a \(\pi \) change in phase;
in moving from one (bright) fringe to the next the thickness of the air film changes by \(\frac{\lambda }{2}\);
in 5.0 cm number of fringes \( = \frac{5}{{0.940}} \times 50 = 266\);
therefore diameter of hair \( = 133 \times 5.92 \times {10^{ - 7}} = 7.87 \times {10^{ - 5}}{\text{ m}}\);
\(80{\text{ }}\mu {\text{m}}\)
Examiners report
A significant number of candidates did not attempt this question or made very poor attempts at answering.
A significant number of candidates did not attempt this question or made very poor attempts at answering.
A significant number of candidates did not attempt this question or made very poor attempts at answering. Candidates who gave good answers often used, correctly, a similar triangles approach to determining the diameter of the hair in part (c).

