| Date | May 2014 | Marks available | 9 | Reference code | 14M.2.HL.TZ2.3 |
| Level | Higher level | Paper | Paper 2 | Time zone | Time zone 2 |
| Command term | Calculate, Explain, Show that, and Sketch | Question number | 3 | Adapted from | N/A |
Question
This question is about binding energy and mass defect.
(i) The nuclear mass of the nuclide helium-3 \(\left( {_2^3{\text{He}}} \right)\) is 3.014931 u. Show that the binding energy per nucleon for the nuclide is about 2.6 MeV.
(ii) The binding energy per nucleon for deuterium \(\left( {_1^2{\text{H}}} \right)\) is 1.11 MeV. Calculate the energy change in the following reaction.
\[_1^2{\text{H}} + _1^1{\text{H}} \to _2^3{\text{HE}} + \gamma \]
(iii) The cross on the grid shows the binding energy per nucleon and nucleon number A of the nuclide nickel-62.
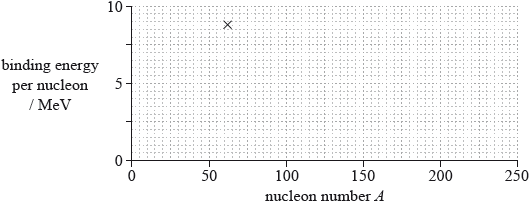
On the grid, sketch a graph to show how the average binding energy per nucleon varies with nucleon number A.
(iv) State and explain, with reference to your sketch graph, whether energy is released or absorbed in the reaction in (b)(ii).
Markscheme
(i) mass defect \(\left( {[2 \times 1.007276 + 1.008665] - 3.014931 = } \right){\text{ }}0.008286{\text{ u}}\);
binding energy per nucleon \(\left( {\frac{{0.008286 \times 931.5}}{3} = } \right)\frac{{7.7}}{3}\)\(\,\,\,\)or\(\,\,\,\)\(2.58{\text{ (MeV)}}\);
(ii) binding energy of left-hand side \( = 1.11 \times 2\) and binding energy of right-hand side \( = 3 \times 2.6\); } (both needed) (allow ECF)
energy release \( = 5.58{\text{ (MeV)}}\); (ignore sign)
(iii) line goes through Ni point and nickel is the maximum ±2 small squares horizontally; } (allow Fe-56 as maximum – this is just outside the range allowed)
line starts at 0, downward trend for A after 62, trend after nickel less steep than before;
Line must go through part of the X to award first marking point.
Line must not flatten out to award second marking point.
Allow smooth curve for low A.
Allow incorrect variations at low A.
(iv) nucleus produced in the reaction is higher up the curve than the reactants / OWTTE; } (must see reference to graph)
reference to binding energy/other valid reason results in energy release;
Award [0] for a bald correct answer.
Award [0] for any discussion of fission.
Examiners report
(i) This relatively easy problem was not well done. There were many permutations of the numbers, and almost all were poorly explained. Completely correct solutions were rare and even these tended to have a poor level of explanation.
(iii) Candidates are required to be able to draw and annotate this plot. This question proved that very many do not appreciate the prominent features. There were mis-drawings on both sides of the maximum; the maximum itself was often misplaced by more than the specified tolerance (showing that candidates do not appreciate the minimum value of the binding energy per nucleon at the Fe-56 or Ni position). Other errors included inappropriate gradients on the right-hand side of the graph compared to the left and failures to begin the curve at the correct place.
(iv) Few candidates referred their knowledge to the graph and simply recalled – often correctly – some physics about the stability of the fusion product. However, this was rarely referred to the relative position of reactants and product on the graph.

