| Date | November 2014 | Marks available | 3 | Reference code | 14N.3.SL.TZ0.2 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Determine | Question number | 2 | Adapted from | N/A |
Question
This question is about standing (stationary) waves.
The diagram shows a tube that is open at both ends.

Point A shows the position of one air molecule in the tube. A standing sound wave (not shown in the diagram) is set up in the tube.
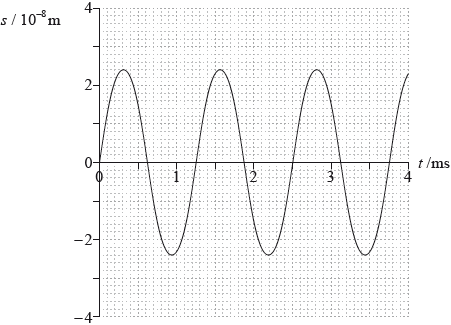
The graph shows the variation of displacement \(s\) with time \(t\) for the molecule at point A.
Outline whether the standing wave is transverse or longitudinal.
The standing wave in the tube corresponds to the fourth harmonic. The speed of sound in the tube is \({\text{340 m}}\,{{\text{s}}^{ - {\text{1}}}}\). Using the graph, determine the length of the tube.
The tube is now closed at one end and the first harmonic is sounded. Outline why the tube that is open at both ends produces a first harmonic with a wavelength shorter than the first harmonic of the tube that is closed at one end.
Markscheme
(longitudinal)
the standing wave is formed of (travelling) sound waves (which are longitudinal);
Do not allow responses that focus only on travelling waves.
the frequency is \(f = \frac{1}{{1.25 \times {{10}^{ - 3}}}}{\text{ }}( = {\text{ }}800{\text{ Hz}})\);
and the wavelength is \(\lambda = \frac{v}{f} = \frac{{340}}{{800}}{\text{ }}( = 0.425{\text{ m}})\);
the fourth harmonic corresponds to 2 wavelengths in the tube, thus \(L = 2\lambda = 0.85{\text{ m}}\);
the length of the tube closed at one end corresponds to \(\frac{\lambda }{4}\), while the length for the tube open at both ends corresponds to \(\frac{\lambda }{2}\);
Examiners report
(a) was very badly answered, with few appreciating that the standing wave is made from 2 (or more) travelling sound waves.
(b) was usually well attempted, with arithmetical errors or errors in the relationship between wavelength and pipe length giving any difficulty.
There was a mixed set of responses to (c), from those who clearly understood to those who could not give a mathematical reason.

