| Date | November 2014 | Marks available | 1 | Reference code | 14N.3.HL.TZ0.22 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Define | Question number | 22 | Adapted from | N/A |
Question
This question is about medical imaging using X-rays.
The table shows the attenuation coefficient \(\mu \) (mu) for different parts of the body.
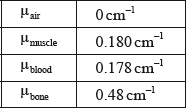
An X-ray scan is taken of a patient to examine the flow of blood through their arm. X-rays of intensity \(I\) are incident on an equal thickness of blood and muscle. The intensity of the X-rays is measured after passing through the blood and muscle respectively.
Define attenuation coefficient.
Calculate the half-value thickness for blood.
Calculate the ratio \(\frac{{{I_{{\text{blood}}}}}}{{{I_{{\text{muscle}}}}}}\) for 1 cm of tissue.
Suggest why an X-ray scan does not allow for the differentiation between muscle and blood.
A contrast medium containing iodine is injected into the patient. This increases the attenuation coefficient of blood so that the difference between the intensities of blood and muscle is greater than 2%. The blood can now be observed on an X-ray scan. Determine the minimum increase in \({\mu _{{\text{blood}}}}\) that will enable a sharper contrast to be observed between an equal thickness of muscle and blood.
X-rays are a form of ionizing radiation. To reduce the danger to a patient, the intensity of X-rays are kept to a minimum. Describe how enhancement allows for low intensity X-rays to be used.
Markscheme
probability of a single photon being absorbed in 1 m of the material / reference to \(I = {I_{\text{o}}}{{\text{e}}^{ - \mu x}}\) with symbols defined;
\({x_{\frac{1}{2}}} = \frac{{\ln 2}}{\mu }\);
\( = 3.89{\text{ cm}}\);
\(\frac{{{I_{{\text{blood}}}}}}{{{I_{{\text{muscle}}}}}} = \frac{{{I_0}{e^{ - {\mu _{{\text{blood}}}}x}}}}{{{I_0}{e^{ - {\mu _{{\text{muscle}}}}x}}}} = \frac{{{e^{ - 0.178x}}}}{{{e^{ - 0.180x}}}}\);
\({e^{0.002}} = 1.002\);
the difference between the intensities is only around 0.2%/less than that (2%) required to provide sufficient contrast between the muscle and the blood;
this is too small to provide a clear difference on the X-ray film;
ratio needs to be 0.98 to show a sharp contrast;
\({e^{(0.180 - {\mu _{{\text{blood}}}})}} = 0.98\);
so \({\mu _{{\text{blood}}}} = 0.2\) / increase of around 0.02;
low intensity X-rays would not provide sufficient contrast between neighbouring tissues;
enhancement shows a clearer difference in the image;
Examiners report
In (a) the definition of physical quantities was better than in previous years.
In (a) the definition of physical quantities was better than in previous years.
In (b)(i), the majority of candidates calculated the ratio of blood/muscle intensities.
In (b)(ii) some candidates did not read the question and answered in terms of blood instead of bone, but better candidates realised that muscle/bone resolution for X-rays is properly and widely used in medical imaging.
In (c) the better candidates applied knowledge in a quite complex situation.
In (d), the better candidates wrote clear answers. Only some candidates described the mechanism of enhancement instead of the role of it.

