| Date | November 2015 | Marks available | 2 | Reference code | 15N.2.SL.TZ0.3 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Sketch | Question number | 3 | Adapted from | N/A |
Question
This question is about simple harmonic motion (SHM).
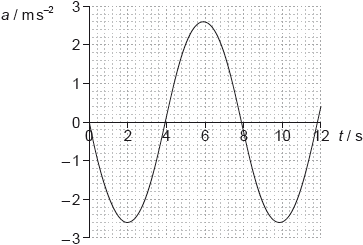
The graph shows the variation with time \(t\) of the acceleration \(a\) of an object X undergoing simple harmonic motion (SHM).
Define simple harmonic motion (SHM).
X has a mass of 0.28 kg. Calculate the maximum force acting on X.
Determine the maximum displacement of X. Give your answer to an appropriate number of significant figures.
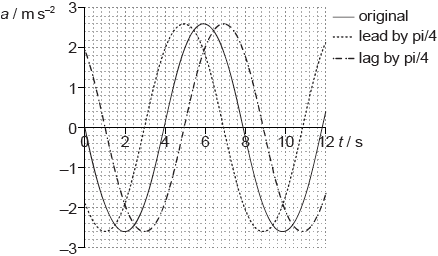
A second object Y oscillates with the same frequency as X but with a phase difference of \(\frac{\pi }{4}\). Sketch, using the graph opposite, how the acceleration of object Y varies with \(t\).
Markscheme
force/acceleration proportional to the displacement/distance from a (fixed/equilibrium) point/mean position;
directed towards this (equilibrium) point / in opposite direction to displacement/ distance;
Allow algebra only if symbols are fully explained.
0.73 (N); (allow answer in range of 0.71 to 0.75 (N))
use of \({a_0} = - {\omega ^2}{x_0}\);
\(T = 7.9{\text{ (s)}}\) or \(\omega = 0.795\) or \(\frac{\pi }{4}{\text{ (rad}}\,{{\text{s}}^{ - 1}})\); } (allow answers in the range of T = 7.8 to 8.0 (s) or \(\omega \) = 0.785 to 0.805 (rad s–1))
\({x_0} = 4.1(1){\text{ (m)}}\); (allow answers in the range of 4.0 to 4.25 (m))
two significant figures in final answer whatever the value;
Award [4] for a bald correct answer.
shape correct, constant amplitude for new curve, minimum of 10 s shown; } (there must be some consistent lead or lag and no change in T)
lead/lag of 1 s (to within half a square by eye);
Examiners report
A good definition of simple harmonic motion must focus on the proportionality between acceleration and displacement from some fixed point and on the directional relationship between acceleration and displacement. Many failed to emphasise the fixed-point aspect of the definition. Attempts made to define simple harmonic motion in algebraic terms normally omitted a clear statement of the symbols and the meaning of the negative sign.
This was almost universally well done.
Similarly, this was well done. Most appreciated the need to truncate the final answer to a sensible number of significant digits (two in this case).
A large number of candidates could not translate a \(\frac{\pi }{4}\) phase change into the correct time lead or lag. Most used the answer for \(\frac{\pi }{2}\) and lost a mark in consequence. Most free-hand sketches of sine curves were acceptable.

