| Date | May 2018 | Marks available | 3 | Reference code | 18M.3.HL.TZ2.10 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Show that | Question number | 10 | Adapted from | N/A |
Question
Two tubes, A and B, are inserted into a fluid flowing through a horizontal pipe of diameter 0.50 m. The openings X and Y of the tubes are at the exact centre of the pipe. The liquid rises to a height of 0.10 m in tube A and 0.32 m in tube B. The density of the fluid = 1.0 × 103 kg m–3.
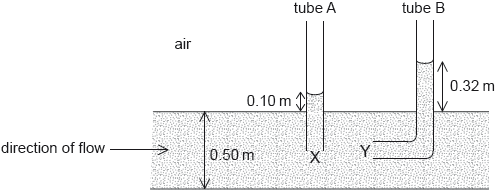
The viscosity of water is 8.9 × 10–4 Pa s.
Show that the velocity of the fluid at X is about 2 ms–1, assuming that the flow is laminar.
Estimate the Reynolds number for the fluid in your answer to (a).
Outline whether your answer to (a) is valid.
Markscheme
\(\frac{1}{2}\rho v_{\text{X}}^2 = {p_{\text{Y}}} - {p_{\text{X}}} = \rho g\Delta h\)
vX = \(\sqrt {2 \times 9.8 \times (0.32 - 0.10)} \)
vx = 2.08 «ms–1»
[3 marks]
R = «\(\frac{{vr\rho }}{\eta } = \frac{{2.1 \times 0.25 \times {{10}^3}}}{{8.9 \times {{10}^{ - 4}}}}\)» 5.9 × 105
[1 mark]
(R > 1000) flow is not laminar, so assumption is invalid
OWTTE
[1 mark]

