| Date | May 2017 | Marks available | 1 | Reference code | 17M.3.HL.TZ2.10 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | State | Question number | 10 | Adapted from | N/A |
Question
A ball is moving in still air, spinning clockwise about a horizontal axis through its centre. The diagram shows streamlines around the ball.
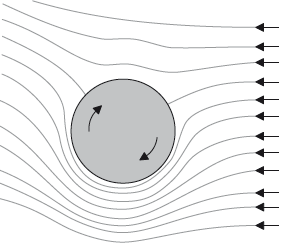
The surface area of the ball is 2.50 x 10–2 m2. The speed of air is 28.4 m\(\,\)s–1 under the ball and 16.6 m\(\,\)s–1 above the ball. The density of air is 1.20 kg\(\,\)m–3.
Estimate the magnitude of the force on the ball, ignoring gravity.
On the diagram, draw an arrow to indicate the direction of this force.
State one assumption you made in your estimate in (a)(i).
Markscheme
Δp = «\(\frac{1}{2}\rho \left( {{v_T}^2 - {v_L}^2} \right) = \frac{1}{2} \times 1.20 \times \left( {{{28.4}^2} - {{16.6}^2}} \right) = \)» 318.6 «Pa»
F = «\(318.6 \times \frac{{2.50 \times {{10}^{ - 2}}}}{4} = \)» 1.99 «N»
Allow ECF from MP1.
[2 marks]
downward arrow of any length or position
Accept any downward arrow not just vertical.
[1 mark]
flow is laminar/non-turbulent
OR
Bernoulli’s equation holds
OR
pressure is uniform on each hemisphere
OR
diameter of ball can be ignored /ρgz = constant
[1 mark]

