| Date | May 2018 | Marks available | 1 | Reference code | 18M.3.HL.TZ1.10 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 1 |
| Command term | Calculate | Question number | 10 | Adapted from | N/A |
Question
The water supply for a hydroelectric plant is a reservoir with a large surface area. An outlet pipe takes the water to a turbine.
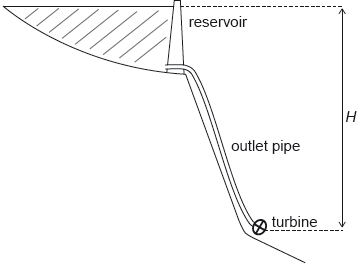
The following data are available:
\[\begin{array}{*{20}{l}} {{\text{density of water}}}&{ = 1.00 \times {{10}^3}{\text{ kg }}{{\text{m}}^{ - 3}}} \\ {{\text{viscosity of water}}}&{ = 1.31 \times {{10}^{ - 3}}{\text{ Pa s}}} \\ {{\text{diameter of the outlet pipe}}}&{ = 0.600{\text{ m}}} \\ {{\text{velocity of water at outlet pipe}}}&{ = 59.4{\text{ m}}{{\text{s}}^{ - 1}}} \end{array}\]
State the difference in terms of the velocity of the water between laminar and turbulent flow.
The water level is a height H above the turbine. Assume that the flow is laminar in the outlet pipe.
Show, using the Bernouilli equation, that the speed of the water as it enters the turbine is given by v = \(\sqrt {2gH} \).
Calculate the Reynolds number for the water flow.
Outline whether it is reasonable to assume that flow is laminar in this situation.
Markscheme
in laminar flow, the velocity of the fluid is constant «at any point in the fluid» «whereas it is not constant for turbulent flow»
Accept any similarly correct answers.
[1 mark]
PS = PT «as both are exposed to atmospheric pressure»
then VT = 0 «if the surface area ofthe reservoir is large»
« \(\frac{1}{2}\rho v_s^2\) + ρgzS = ρgzT»
\(\frac{1}{2}v_S^2\) = g(zT – zS) = gH
and so vS = \(\sqrt {2gH} \)
MP1 and MP2 may be implied by the correct substitution showing line 3 in the mark scheme.
Do not accept simple use of v = \(\sqrt {2{\text{as}}} \).
[3 marks]
R = \(\frac{{59.4 \times 0.6 \times 1 \times {{10}^3}}}{{1.31 \times {{10}^{ - 3}}}}\) = 2.72 × 107
Accept use of radius 0.3 m giving value 1.36 × 107.
[1 mark]
as R > 1000 it is not reasonable to assume laminar flow
[1 mark]

