| Date | May 2018 | Marks available | 2 | Reference code | 18M.3.HL.TZ1.19 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 1 |
| Command term | Draw | Question number | 19 | Adapted from | N/A |
Question
A galaxy can be modelled as a sphere of radius R0. The distance of a star from the centre of the galaxy is r.
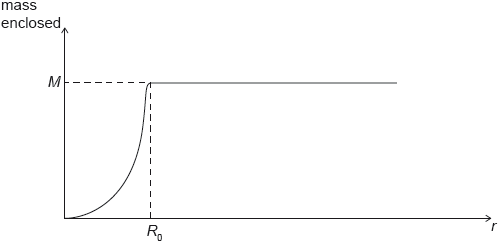
For this model the graph is a simplified representation of the variation with r of the mass of visible matter enclosed inside r.
The mass of visible matter in the galaxy is M.
Show that for stars where r > R0 the velocity of orbit is v = \(\sqrt {\frac{{GM}}{r}} \).
Draw on the axes the observed variation with r of the orbital speed v of stars in a galaxy.
Explain, using the equation in (a) and the graphs, why the presence of visible matter alone cannot account for the velocity of stars when r > R0.
Markscheme
\(\frac{{m{v^2}}}{r} = \frac{{GMm}}{{{r^2}}}\) and correct rearranging
[1 mark]
linear / rising until R0
then «almost» constant
[2 marks]
for v to stay constant for r greater than R0, M has to be proportional to r
but this contradicts the information from the M-r graph
OR
if M is constant for r greater than R0, then we would expect v \( \propto {r^{\frac{{ - 1}}{2}}}\)
but this contradicts the information from the v-r graph
[2 marks]

