| Date | May 2017 | Marks available | 1 | Reference code | 17M.3.HL.TZ1.17 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 1 |
| Command term | Draw | Question number | 17 | Adapted from | N/A |
Question
Recent evidence from the Planck observatory suggests that the matter density of the universe is ρm = 0.32 ρc, where ρc ≈ 10–26 kg\(\,\)m–3 is the critical density.
The graph shows the variation with time t of the cosmic scale factor R in the flat model of the universe in which dark energy is ignored.
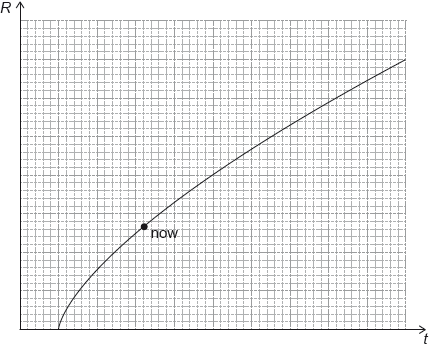
On the axes above draw a graph to show the variation of R with time, when dark energy is present.
The density of the observable matter in the universe is only 0.05 ρc. Suggest how the remaining 0.27 ρc is accounted for.
The density of dark energy is ρΛc2 where ρΛ = ρc – ρm. Calculate the amount of dark energy in 1 m3 of space.
Markscheme
curve starting earlier, touching at now and going off to infinity
[1 mark]
there is dark matter that does not radiate / cannot be observed
Unexplained mention of "dark matter" is not sufficient for the mark.
[1 mark]
ρΛ = 0.68ρc = 0.68 × 10−26 «kgm−3»
energy in 1 m3 is therefore 0.68 × 10−26 × 9 × 1016 ≈ 6 × 10−10 «J»
[2 marks]

