| Date | May 2018 | Marks available | 2 | Reference code | 18M.3.HL.TZ1.7 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 1 |
| Command term | Explain | Question number | 7 | Adapted from | N/A |
Question
An observer A is on the surface of planet X. Observer B is in a stationary spaceship above the surface of planet X.
Observer A sends a beam of light with a frequency 500 THz towards observer B. When observer B receives the light he observes that the frequency has changed by Δf.
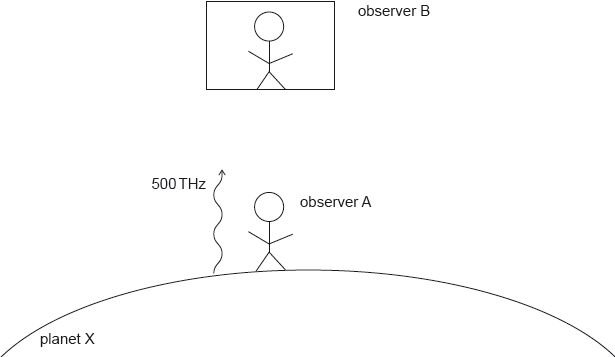
Observer B then sends a signal with frequency 1500 THz towards observer A.
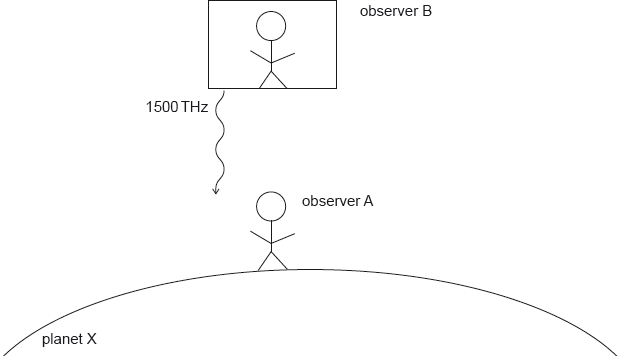
Calculate the shift in frequency observed by A in terms of Δf.
Calculate the gravitational field strength on the surface of planet X.
The following data is given:
Δf = 170 Hz.
The distance between observer A and B is 10 km.
Observer A now sends a beam of light initially parallel to the surface of the planet.
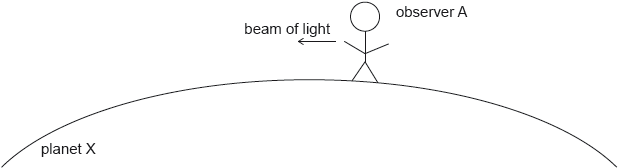
Explain why the path of the light is curved.
Markscheme
Δf \( \propto \) f
therefore the change is «–»3Δf
[2 marks]
g = «c2 \(\frac{{\Delta f}}{{f\Delta h}}\) =» (3 × 108)2\(\frac{{170}}{{5.0 \times {{10}^{14}} \times 10\,000}}\)
g = 3.1 «ms–2»
If POT mistake, award [0].
Award [2] for BCA.
[2 marks]
the mass of the planet warps spacetime around itself
the light will follow the shortest path in spacetime «which is curved»
[2 marks]

