| Date | November 2010 | Marks available | 3 | Reference code | 10N.3.HL.TZ0.H3 |
| Level | Higher level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Explain and State | Question number | H3 | Adapted from | N/A |
Question
This question is about general relativity.
Bob is standing on the floor of a spaceship and he throws a ball in a direction parallel to the floor.
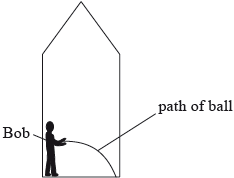
Between leaving Bob’s hand and landing on the floor, the ball follows the path shown.
State and explain whether, from the path followed by the ball, Bob can deduce that the spaceship is at rest on the surface of a planet.
Outline how the concept of spacetime can be used to explain the
(i) trajectory of the ball if the spaceship is at rest on the surface of a planet.
(ii) nature of a black hole.
Calculate the radius that Earth would have to have in order for it to behave as a black hole. The mass of Earth is \(6.0 \times {10^{24}}{\text{ kg}}\).
Markscheme
no
it could be accelerating (upwards);
because of the principle of equivalence;
that states there is no way that gravitational effects can be distinguished from inertial effects;
(i) the planet warps spacetime;
and the ball follows the shortest path in spacetime;
(ii) the black hole causes extreme curvature of spacetime;
any light leaving the surface will be bent back to the surface of the black hole / OWTTE;
8.8 mm or \(8.8 \times {10^{ - 3}}{\text{ m}}\);
Examiners report
Generally speaking, candidates had much more success with this question.
Generally speaking, candidates had much more success with this question although the ideas of the shortest path in space time in (b)(i) and of extreme curvature in (b)(ii) were often missed.
The substitution was usually done correctly.

