| Date | May 2018 | Marks available | 3 | Reference code | 18M.3.SL.TZ2.6 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Show that | Question number | 6 | Adapted from | N/A |
Question
A wheel of mass 0.25 kg consists of a cylinder mounted on a central shaft. The shaft has a radius of 1.2 cm and the cylinder has a radius of 4.0 cm. The shaft rests on two rails with the cylinder able to spin freely between the rails.
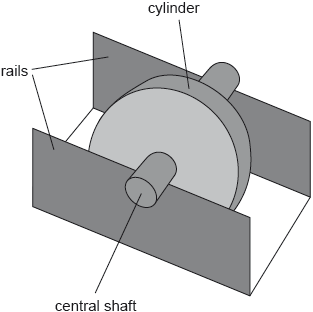
The stationary wheel is released from rest and rolls down a slope with the shaft rolling on the rails without slipping from point A to point B.
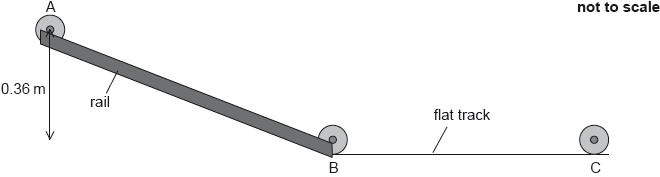
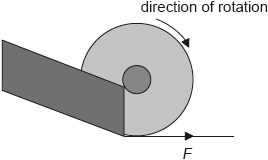
The wheel leaves the rails at point B and travels along the flat track to point C. For a short time the wheel slips and a frictional force F exists on the edge of the wheel as shown.
The moment of inertia of the wheel is 1.3 × 10–4 kg m2. Outline what is meant by the moment of inertia.
In moving from point A to point B, the centre of mass of the wheel falls through a vertical distance of 0.36 m. Show that the translational speed of the wheel is about 1 m s–1 after its displacement.
Determine the angular velocity of the wheel at B.
Describe the effect of F on the linear speed of the wheel.
Describe the effect of F on the angular speed of the wheel.
Markscheme
an object’s resistance to change in rotational motion
OR
equivalent of mass in rotational equations
OWTTE
[1 mark]
ΔKE + Δrotational KE = ΔGPE
OR
\(\frac{1}{2}\)mv2 + \(\frac{1}{2}\)I\(\frac{{{v^2}}}{{{r^2}}}\) = mgh
\(\frac{1}{2}\) × 0.250 × v2 + \(\frac{1}{2}\) × 1.3 × 10–4 × \(\frac{{{v^2}}}{{1.44 \times {{10}^{ - 4}}}}\) = 0.250 × 9.81 × 0.36
v = 1.2 «m s–1»
[3 marks]
ω «= \(\frac{{1.2}}{{0.012}}\)» = 100 «rad s–1»
[1 mark]
force in direction of motion
so linear speed increases
[2 marks]
force gives rise to anticlockwise/opposing torque on
wheel ✓ so angular speed decreases ✓
OWTTE
[2 marks]

