| Date | May 2018 | Marks available | 2 | Reference code | 18M.3.SL.TZ1.6 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 1 |
| Command term | Explain | Question number | 6 | Adapted from | N/A |
Question
A constant force of 50.0 N is applied tangentially to the outer edge of a merry-go-round. The following diagram shows the view from above.
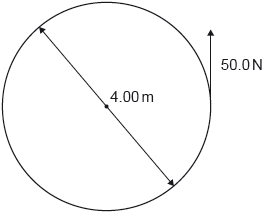
The merry-go-round has a moment of inertia of 450 kg m2 about a vertical axis. The merry-go-round has a diameter of 4.00 m.
The merry-go-round starts from rest and the force is applied for one complete revolution.
A child of mass 30.0 kg is now placed onto the edge of the merry-go-round. No external torque acts on the system.
The child now moves towards the centre.
Show that the angular acceleration of the merry-go-round is 0.2 rad s–2.
Calculate, for the merry-go-round after one revolution, the angular speed.
Calculate, for the merry-go-round after one revolution, the angular momentum.
Calculate the new angular speed of the rotating system.
Explain why the angular speed will increase.
Calculate the work done by the child in moving from the edge to the centre.
Markscheme
Γ «= Fr = 50 × 2» = 100 «Nm»
α « \( = \frac{\Gamma }{I} = \frac{{100}}{{450}}\) » =0.22 «rads–2»
Final value to at least 2 sig figs, OR clear working with substitution required for mark.
[2 marks]
«\(\omega _t^2 - \omega _0^2 = 2\alpha \Delta \theta \)»
«\(\omega _t^2 - 0 = 2 \times 0.22 \times 2\pi \)»
\({\omega _t} = 1.7\) «rads–1»
Accept BCA, values in the range: 1.57 to 1.70.
[1 mark]
«L = Iω = 450 × 1.66»
= 750 «kgm2 rads–1»
Accept BCA, values in the range: 710 to 780.
[1 mark]
«I = 450 + mr2»
I «= 450 + 30 × 22» = 570 «kgm2»
«L = 570 × ω = 747»
ω = 1.3 «rads–1»
Watch for ECF from (a) and (b).
Accept BCA, values in the range: 1.25 to 1.35.
[2 marks]
moment of inertia will decrease
angular momentum will be constant «as the system is isolated»
«so the angular speed will increase»
[2 marks]
ωt = 1.66 from bi AND W = ΔEk
W = \(\frac{1}{2}\) × 450 × 1.662 – \(\frac{1}{2}\) × 570 × 1.312 = 131 «J»
ECF from 8bi
Accept BCA, value depends on the answers in previous questions.
[2 marks]

