| Date | May 2012 | Marks available | 3 | Reference code | 12M.2.hl.TZ2.3 |
| Level | HL | Paper | 2 | Time zone | TZ2 |
| Command term | Calculate and Identify | Question number | 3 | Adapted from | N/A |
Question
Lattice enthalpies can be determined experimentally using a Born–Haber cycle and theoretically using calculations based on electrostatic principles.
The experimental lattice enthalpies of the chlorides of lithium, LiCl, sodium, NaCl, potassium, KCl, and rubidium, RbCl, are given in Table 13 of the Data Booklet. Explain the trend in the values.
Explain why magnesium chloride, \({\text{MgC}}{{\text{l}}_{\text{2}}}\), has a much greater lattice enthalpy than sodium chloride, NaCl.
(i) Identify the process labelled a on the Born–Haber cycle for the determination of the standard enthalpy of formation of lithium fluoride, LiF.
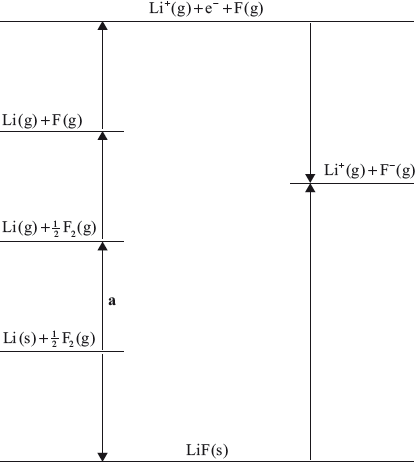
(ii) The enthalpy change for process a is \( + 159{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\). Calculate the standard enthalpy of formation of lithium fluoride, LiF, using this and other values from the Data Booklet.
Markscheme
radius of the metal/positive ion/cation increases;
attraction (between ions) is weaker;
higher charge (on cation);
smaller radius (of cation);
(i) (standard enthalpy of) atomization/\(\Delta H_{{\text{atomization}}}^\Theta \) / (standard enthalpy of) sublimation/\(\Delta H_{{\text{sublimation}}}^\Theta \);
(ii) \(\begin{array}{*{20}{l}} {{\text{lattice enthalpy}} = + 1049{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}}&{{\text{(Data Booklet Table 13)}}} \\ {{\text{bond enthalpy F}}--{\text{F}} = + 158{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}}&{{\text{(Data Booklet Table 10)}}} \\ {{\text{first ionization energy (Li)}} = + 520{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}}&{{\text{(Data Booklet Table 7)}}} \\ {\Delta H_{{\text{electron affinity}}}^\Theta {\text{(F)}} = - 328{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}}&{{\text{(Data Booklet Table 7)}}} \\ {\Delta H_{{\text{atomization}}}^\Theta {\text{ of Li}} = + 159{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}}&{{\text{(given)}}} \end{array}\)
\(\Delta H_{\text{f}}^\Theta = + 159 + \frac{1}{2}(158) + 520 + ( - 328) - (1049)\);
\( = - 619{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\);
Accept use of theoretical value of lattice enthalpy, +1030 kJ mol–1:
\(\Delta H_{\text{f}}^\Theta = + \)159 \( + \frac{1}{2}\)(158) \( + \) 520 \( + \) (–328) – (1030)
= –600 kJ\(\,\)mol–1
Examiners report
Many candidates had difficulty correctly explaining the trends in lattice enthalpy values in (a), referring to atomic radii or the attraction between the metal nucleus and valence or bonding electrons, and giving explanations that sounded like descriptions of first ionization energy or covalent bonding.
In (b) most candidates scored one mark for stating that the Mg ion has a greater charge than Na ion. Few also mentioned that the size of the Mg ion is less than the Na ion.
Most candidates correctly identified sublimation or atomization of Li in (c)(i). Vaporization was the most common error. In (c)(ii), many candidates forgot to divide the bond enthalpy of fluorine by 2. Some had difficulty finding the enthalpy of atomization of fluorine in the Data Booklet, and some obtained all the correct values but did not put the correct signs on the values when using Hess‘s Law.

