| Date | May 2012 | Marks available | 9 | Reference code | 12M.2.hl.TZ0.1 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
The area of an equilateral triangle is \(1\) cm2. Determine the area of:
The points A, B have coordinates (\(1\), \(0\)), (\(0\), \(1\)) respectively. The point P(\(x\), \(y\)) moves in such a way that \({\rm{AP}} = k{\rm{BP}}\) where \(k \in {\mathbb{R}^ + }\) .
the circumscribed circle.
the inscribed circle.
When \(k = 1\) , show that the locus of P is a straight line.
When \(k \ne 1\) , the locus of P is a circle.
(i) Find, in terms of \(k\) , the coordinates of C, the centre of this circle.
(ii) Find the equation of the locus of C as \(k\) varies.
Markscheme
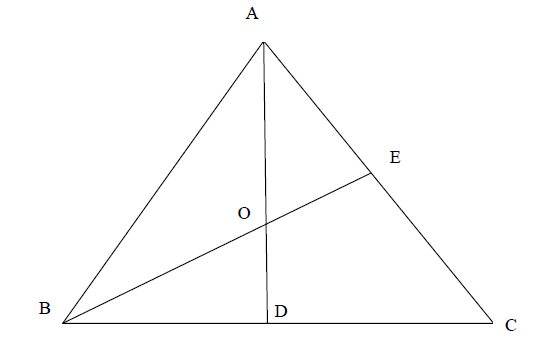
consider the above diagram – [AD] and [BE] are the medians and O is therefore both the incentre and the circumcentre (R1)
let \({\rm{AB}} = d\) and let \(R\) denote the radius of the circumcircle
then,
\(R = {\rm{AO}} = {\rm{AE}}\sec {30^ \circ }\) M1
\( = \frac{d}{2} \times \frac{2}{{\sqrt 3 }} = \frac{d}{{\sqrt 3 }}\) (A1)
area of circumcircle \( = \pi {R^2} = \frac{{\pi {d^2}}}{3}\) A1
area of triangle \({\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{AB}}{\rm{.AC}}\sin {\rm{BAC}}\) M1
\( = \frac{{\sqrt 3 {d^2}}}{4}\) (A1)
\(\frac{{\sqrt 3 {d^2}}}{4} = 1 \Rightarrow {d^2} = \frac{4}{{\sqrt 3 }}\) A1
area of circumcircle \( = \frac{{4\pi }}{{3\sqrt 3 }}\) (\(2.42\)) A1
[8 marks]
let \(r\) denote the radius of the incircle
then
\(r = {\rm{OE}} = {\rm{AE}}\tan {30^ \circ }\) M1
\( = \frac{d}{{2\sqrt 3 }}\) (A1)
area of incircle \( = \pi {r^2} = \frac{{\pi {d^2}}}{{12}}\)
\( = \frac{\pi }{{3\sqrt 3 }}\) (\(0.605\)) A1
[3 marks]
\({\rm{A}}{{\rm{P}}^2} = {(x - 1)^2} + {y^2}\) and \({\rm{B}}{{\rm{P}}^2} = {x^2} + {(y - 1)^2}\) A1
\({x^2} - 2x + 1 + {y^2} = {x^2} + {y^2} - 2y + 1\) M1
\(y = x\) which is the equation of a straight line A1
[3 marks]
(i) \({x^2} - 2x + 1 + {y^2} = {k^2}({x^2} + {y^2} - 2y + 1)\) M1
\(({k^2} - 1){x^2} + ({k^2} - 1){y^2} + 2x - 2{k^2}y + {k^2} - 1 = 0\) A1
\({x^2} + {y^2} + \frac{{2x}}{{{k^2} - 1}} - \frac{{2{k^2}y}}{{{k^2} - 1}} + 1 = 0\) A1
by completing the squares or quoting the standard result, M1
coordinates of C are
\(\left( { - \frac{1}{{{k^2} - 1}},\frac{{{k^2}}}{{{k^2} - 1}}} \right)\) A1
(ii) let (\(x\), \(y\)) be the coordinates of C
attempting to find \(k\) or \({{k^2}}\) , (M1)
\({k^2} = 1 - \frac{1}{x}\) (A1)
\(y = \frac{{1 - \frac{1}{x}}}{{ - \frac{1}{x}}}\) (M1)
\(y = 1 - x\) A1
[9 marks]
Examiners report
Most candidates attempted (a) with many different methods seen although some candidates made algebraic errors in applying the appropriate trigonometrical formulae.
Very few candidates realised that, because the centre of the triangle divides an altitude in the ratio \(2:1\), the area of the inscribed circle is one quarter the area of the circumscribed circle.
Most candidates solved (a) correctly.
Solutions to (b) were often disappointing. Those candidates who used coordinate geometry often made algebraic errors in obtaining the equation of the circle and then finding the coordinates of its centre. Some candidates tried to use Apollonius’ theorem, using the fact that the centre divides the line AB in a ratio dependent upon \(k\), but this approach almost invariably led to algebraic errors.

