| Date | May 2015 | Marks available | 3 | Reference code | 15M.1.hl.TZ0.10 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
A wheel of radius \(r\) rolls, without slipping, along a straight path with the plane of the wheel remaining vertical. A point \({\text{A}}\) on the circumference of the wheel is initially at \({\text{O}}\). When the wheel is rolled, the radius rotates through an angle of \(\theta \) and the point of contact is now at \({\text{B}}\), where the length of the arc \({\text{AB}}\) is equal to the distance \({\text{OB}}\). This is shown in the following diagram.
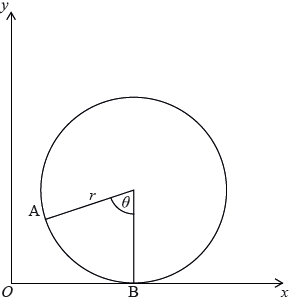
Find the coordinates of \({\text{A}}\) in terms of \(r\) and \(\theta \).
As the wheel rolls, the point A traces out a curve. Show that the gradient of this curve is \(\cot \left( {\frac{1}{2}\theta } \right)\).
Find the equation of the tangent to the curve when \(\theta = \frac{\pi }{3}\).
Markscheme
\({\text{OX}} = {\text{OB}} - {\text{XB}} = r\theta - r\sin \theta = x\) (M1)A1
\({\text{OY}} = {\text{ZB}} - {\text{ZC}} = r - r\cos \theta = y\) A1
\(\frac{{{\text{d}}x}}{{{\text{d}}\theta }} = r - r\cos \theta \) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}\theta }} = r\sin \theta \) A1
\(\frac{{{\text{d}}y}}{{{\text{d}}x}} = \frac{{r\sin \theta }}{{r - r\cos \theta }}\) M1
\( = \frac{{2\sin \frac{\theta }{2}\cos \frac{\theta }{2}}}{{2{{\sin }^2}\frac{\theta }{2}}}\) M1A1A1
\( = \frac{{\cos \frac{\theta }{2}}}{{\sin \frac{\theta }{2}}}\)
\( = \cot \frac{\theta }{2}\) AG
when \(\theta = \frac{\pi }{3}\), gradient \( = \sqrt 3 \) A1
\(x = \frac{\pi }{3}r - r\frac{{\sqrt 3 }}{2},{\text{ }}y = r - \frac{r}{2} = \frac{r}{2}\) A1
\(y - \frac{r}{2} = \sqrt 3 \left( {x - \frac{\pi }{3}r + r\frac{{\sqrt 3 }}{2}} \right)\;\;\;{\text{or}}\;\;\;y = \sqrt 3 x + 2r - \frac{{\pi r}}{{\sqrt 3 }}\) A1
Examiners report
Many candidates were unable to find the coordinates of the point A which made (b) inaccessible. Many candidates reached the halfway point in (b) but were then unable to use the half angle formulae to obtain the required result. Many of the candidates who failed to solve (b) picked up the A1 in (c) for finding the gradient.
Many candidates were unable to find the coordinates of the point A which made (b) inaccessible. Many candidates reached the halfway point in (b) but were then unable to use the half angle formulae to obtain the required result. Many of the candidates who failed to solve (b) picked up the A1 in (c) for finding the gradient.
Many candidates were unable to find the coordinates of the point A which made (b) inaccessible. Many candidates reached the halfway point in (b) but were then unable to use the half angle formulae to obtain the required result. Many of the candidates who failed to solve (b) picked up the A1 in (c) for finding the gradient.

