| Date | May 2008 | Marks available | 4 | Reference code | 08M.1.hl.TZ0.1 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find and Write down | Question number | 1 | Adapted from | N/A |
Question
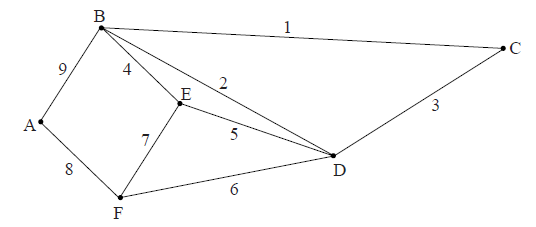
The above diagram shows the weighted graph \(G\).
Determine whether or not \(G\) is bipartite.
[2]
a.
(i) Write down the adjacency matrix for \(G\).
(ii) Find the number of distinct walks of length \(4\) beginning and ending at A.
[4]
b.
Markscheme
\(G\) is bipartite A1
because it contains a triangle. R1
Note: Award R1 for a valid attempt at showing that the vertices cannot be divided into two disjoint sets.
[2 marks]
a.
(i)
\({\boldsymbol{M}} = \left( {\begin{array}{*{20}{c}}
0&1&0&0&0&1 \\
1&0&1&1&1&0 \\
0&1&0&1&0&0 \\
0&1&1&0&1&1 \\
0&1&0&1&0&1 \\
1&0&0&1&1&0
\end{array}} \right)\) A1
(ii) We require the (A, A) element of \({\boldsymbol{M}^4}\) which is \(13\). M1A2
[4 marks]
b.
Examiners report
[N/A]
a.
[N/A]
b.
