| Date | May 2011 | Marks available | 2 | Reference code | 11M.2.hl.TZ0.1 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Write down | Question number | 1 | Adapted from | N/A |
Question
A canal system divides a city into six land masses connected by fifteen bridges, as shown in the diagram below.
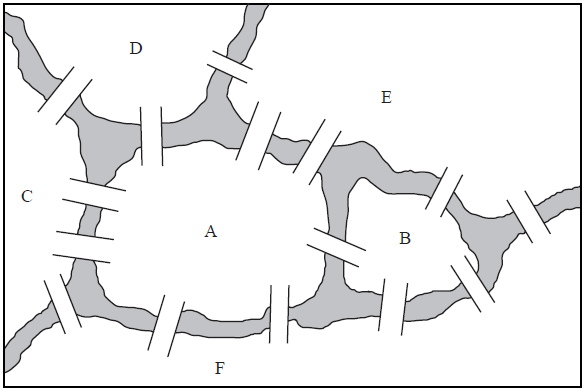
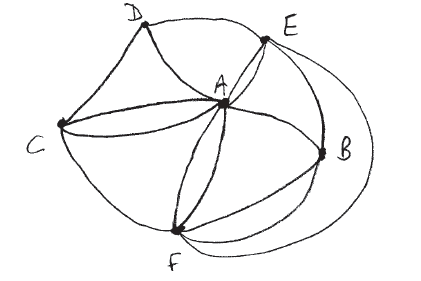
Draw a planar graph to represent this map.
Write down the adjacency matrix of the graph.
List the degrees of each of the vertices.
State with reasons whether or not this graph has
(i) an Eulerian circuit;
(ii) an Eulerian trail.
Find the number of walks of length \(4\) from E to F.
Markscheme
 A2
A2
[2 marks]
 A2
A2
Note: Award A1 for one error or omission, A0 for more than one error or omission. Two symmetrical errors count as one error.
[2 marks]
A B C D E F
(8, 4, 4, 3, 5, 6) A2
[2 marks]
(i) no, because there are odd vertices M1A1
(ii) yes, because there are exactly two odd vertices M1A1
[4 marks]
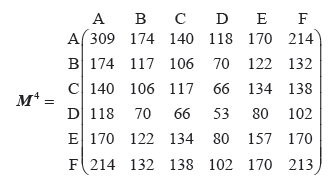
number of walks of length \(4\) is \(170\) (M1)A1
Note: The complete matrix need not be shown. Only one of the FE has to be shown.
[2 marks]
Examiners report
Parts (a) to (c) and (e) did not prove unusually difficult and were answered well.
Parts (a) to (c) and (e) did not prove unusually difficult and were answered well.
Parts (a) to (c) and (e) did not prove unusually difficult and were answered well.
Part (d) proved more problematic since there was confusion between the conditions to be satisfied for there to be a circuit and a trail. There is a difference between "there are two odd vertices" and "there are exactly two odd vertices". As noted elsewhere on paper 1, appreciation of the restrictions as well as the applications of results in mathematics should both be emphasized.
Parts (a) to (c) and (e) did not prove unusually difficult and were answered well. Not all of the matrix in part (e) needed to be shown.

