| Date | May 2013 | Marks available | 7 | Reference code | 13M.2.hl.TZ0.4 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Question number | 4 | Adapted from | N/A |
Question
A group of people: Andrew, Betty, Chloe, David, Edward, Frank and Grace, has certain mutual friendships:
Andrew is friendly with Betty, Chloe, David and Edward;
Frank is friendly with Betty and Grace;
David, Chloe and Edward are friendly with one another.
(i) Draw the planar graph \(H\) that represents these mutual friendships.
(ii) State how many faces this graph has.
Determine, giving reasons, whether \(H\) has
(i) a Hamiltonian path;
(ii) a Hamiltonian cycle;
(iii) an Eulerian circuit;
(iv) an Eulerian trail.
Verify Euler’s formula for \(H\) .
State, giving a reason, whether or not \(H\) is bipartite.
Write down the adjacency matrix for \(H\) .
David wishes to send a message to Grace, in a sealed envelope, through mutual friends.
In how many different ways can this be achieved if the envelope is passed seven times and Grace only receives it once?
Markscheme
(i)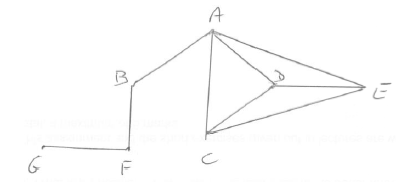
A2
Note: Award A1 if one error made.
(ii) \(4\) A1
[3 marks]
(i) yes, for example GFBACDE A1R1
(ii) no, for example F and B would be visited twice A1R1
(iii) no, because the graph contains vertices of odd degree A1R1
(iv) no, because there are more than two vertices of odd degree A1R1
Note: The A and R marks can be considered as independent.
[8 marks]
\(v = 7\) , \(e = 9\) A1
\(f = 4\) from (a)(ii)
\(9 + 2 = 7 + 4\) R1AG
[2 marks]
no, because the graph contains at least one triangle A1R1
[2 marks]
\(\left( {\begin{array}{*{20}{c}}
{}&{\text{A}}&{\text{B}}&{\text{C}}&{\text{D}}&{\text{E}}&{\text{F}}&{\text{G}} \\
{\text{A}}&0&1&1&1&1&0&0 \\
{\text{B}}&1&0&0&0&0&1&0 \\
{\text{C}}&1&0&0&1&1&0&0 \\
{\text{D}}&1&0&1&0&1&0&0 \\
{\text{E}}&1&0&1&1&0&0&0 \\
{\text{F}}&0&1&0&0&0&0&1 \\
{\text{G}}&0&0&0&0&0&1&0
\end{array}} \right)\) A2
Note: A1 for one error, A0 for more than one error.
[2 marks]
METHOD 1
DG element of 7th power of matrix \( = 26\) M1A1A1
Note: M1 for attempt at some power; A1 for 7th power; A1 for \(26\).
DG element of the 5th power of the matrix \( = 2\) A1A1
obtain \(26 - 2 = 24\) M1A1
METHOD 2
the observation that letter has to reach Grace after Frank obtains it after \(6\) passings, (without Grace having received it earlier) (M1)(A1)
statement that the G row and column have been deleted A1A1
DF element of 6th power of new matrix is \(24\) M1A1A1
Note: M1 for attempt at some power of new or old matrix; A1 for 6th power of new matrix; A1 for 24.
[7 marks]
Examiners report
This question was generally well done.
This question was generally well done. Candidates who lost marks tended to do so as follows: (b)(i) for failing to give an example of a Hamiltonian path; (b)(ii) for giving an incomplete reason for the non-existence of a Hamiltonian cycle; (b)(iii)(iv) for giving the same reason for both parts.
This question was generally well done.
This question was generally well done. Candidates who lost marks tended to do so as follows: (d) for giving the definition of a bipartite graph as the reason for the fact that \(H\) is not bipartite.
This question was generally well done.
This question was generally well done.

