| Date | May 2017 | Marks available | 7 | Reference code | 17M.2.hl.TZ0.1 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 1 | Adapted from | N/A |
Question
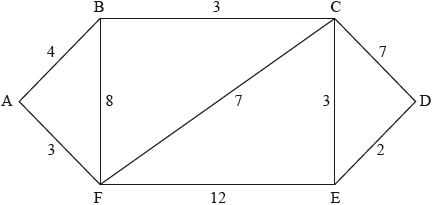
The diagram shows the graph \(G\) with the weights of the edges marked.
State what features of the graph enable you to state that \(G\) contains an Eulerian trail but no Eulerian circuit.
Write down an Eulerian trail.
Use Dijkstra’s algorithm to find the path of minimum total weight joining A to D, stating this total weight. Your solution should show clearly that this algorithm has been used.
Markscheme
there is an Eulerian trail because \(G\) contains exactly two vertices of odd order A1
there is no Eulerian circuit because \(G\) contains vertices of odd order A1
[2 marks]
the trail must start at B and end at E (or vice versa) (R1)
BAFBCFECDE R1
[2 marks]

Note: Award full marks if the correct path is given with correct total weight if an annotated graph is given that represents the Dijkstra algorithm.
[7 marks]

