| Date | May 2012 | Marks available | 6 | Reference code | 12M.2.hl.TZ0.2 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Determine and Find | Question number | 2 | Adapted from | N/A |
Question
The graph \(H\) has the following adjacency matrix.

(i) Show that \(H\) is bipartite.
(ii) Draw \(H\) as a planar graph.
(i) Explain what feature of \(H\) guarantees that it has an Eulerian circuit.
(ii) Write down an Eulerian circuit in \(H\) .
(i) Find the number of different walks of length five joining A to B.
(ii) Determine how many of these walks go through vertex F after passing along two edges.
Find the maximum number of extra edges that can be added to \(H\) while keeping it simple, planar and bipartite.
Find the smallest positive integer \(m\) such that \({3^m} \equiv 1(\bmod 22)\) .
Given that \({3^{49}} \equiv n(\bmod 22)\) where \(0 \le n \le 21\) , find the value of \(n\) .
Solve the equation \({3^x} \equiv 5(\bmod 22)\) .
Markscheme
(i) using any method, (M1)
find that \(\left\{ {{\rm{A,C,D,F}}} \right\}\) and \(\left\{ {{\rm{B,E,G}}} \right\}\) are disjoint sets of vertices A1
so that \(H\) is bipartite AG
(ii)
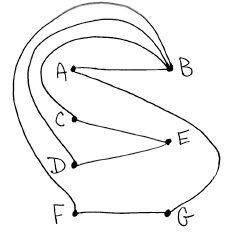 A1
A1
[3 marks]
(i) all vertices are of even degree A1
(ii) DECBAGFBD A2
[3 marks]
(i) M1
M1
number of walks \( = 36\) A1
(ii) recognition of the need to find walks of length \(2\) and walks of length \(3\) (M1)
number of walks of length \(2\) from A to F \( = 2\) A1
number of walks of length \(3\) from F to B \( = 6\) A1
required number of walks \( =12\) A1
[6 marks]
for a simple, bipartite graph to be planar,
\(e \le 2v - 4 = 10\) M1
at the moment, \(e = 8\) which means that we cannot add more than \(2\) edges A1
we see that we can add \(2\) edges, e.g. EA and EF A1
the maximum number of edges we can add is therefore \(2\) A1
[4 marks]
evaluating successive powers of \(3\) (M1)
\({3^1} \equiv 3(\bmod 22)\) , \({3^2} \equiv 9(\bmod 22)\) , \({3^3} \equiv 5(\bmod 22)\)
\({3^4} \equiv 15(\bmod 22)\) , \({3^5} \equiv 1(\bmod 22)\) so \(m = 5\) A1
[2 marks]
since \({3^5} \equiv 1(\bmod 22)\) , \({3^{45}} = {({3^5})^9} \equiv 1(\bmod 22)\) M1A1
consider \({3^{49}} = {3^{45}} \times {3^4} \equiv 1 \times 15(\bmod 22)\) so \(n = 15\) M1A1
[4 marks]
from (a), \(x = 3\) is a solution A1
since \({3^5} \equiv 1(\bmod 22)\) , the complete solution is \(x = 3 + 5N\) where \(N \in \bullet \) (M1)A1
[3 marks]
Examiners report
Solutions to (a) and (b) were generally satisfactory.
Solutions to (a) and (b) were generally satisfactory.
In (c)(ii), few candidates realised that they had to find the number of walks of length two joining A to F, the number of walks of length three joining F to B and then multiply these two numbers together.
In (d), most candidates noted that the number of edges, \(e\), was equal to \(8\) and that application of the inequality \(e \le 2v - 4\) gave \(e \le 10\) . They therefore concluded that two more edges could be drawn. It is, however, important to realise that the value of \(e\) given by this inequality is an upper bound that may not be attainable and that in this case, it was necessary to show that two extra edges could in fact be drawn.
This question was well answered in general with a variety of methods seen. Most candidates realised that the numbers involved precluded the use of Fermat’s little theorem.
This question was well answered in general with a variety of methods seen. Most candidates realised that the numbers involved precluded the use of Fermat’s little theorem.
In (c), most candidates gave \(x = 3\) as a solution following their earlier work in (a) but many candidates failed to realise that their answer to (b) showed that the general solution to (c) was actually \(3 + 5N\) where \(N\) is a non negative integer.

