| Date | May 2010 | Marks available | 3 | Reference code | 10M.2.hl.TZ0.3 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Explain and Write down | Question number | 3 | Adapted from | N/A |
Question
The following diagram shows a weighted graph \(G\) .
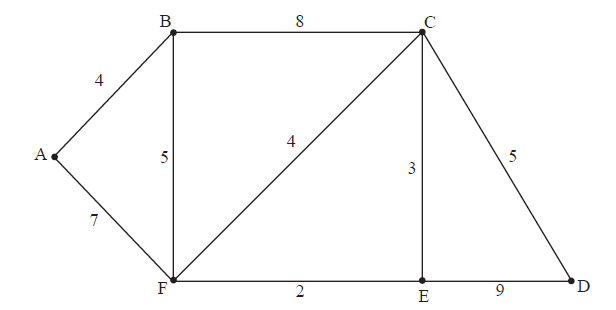
(i) Explain briefly what features of the graph enable you to state that \(G\) has an Eulerian trail but does not have an Eulerian circuit.
(ii) Write down an Eulerian trail in \(G\) .
(i) Use Kruskal’s algorithm to find and draw the minimum spanning tree for \(G\) . Your solution should indicate the order in which the edges are added.
(ii) State the weight of the minimum spanning tree.
Use Dijkstra’s algorithm to find the path of minimum total weight joining A to D, and state its weight. Your solution should indicate clearly the use of this algorithm.
Markscheme
(i) \(G\) has an Eulerian trail because it has \(2\) vertices of odd degree and the remaining vertices of even degree R1
\(G\) does not have an Eulerian circuit because not all vertices are of even degree R1
(ii) BAFBCFECDE A1
[3 marks]
(i) the edges are added in the order
FE A1
CE
AB A1
BF, CD
or CD, BF A1
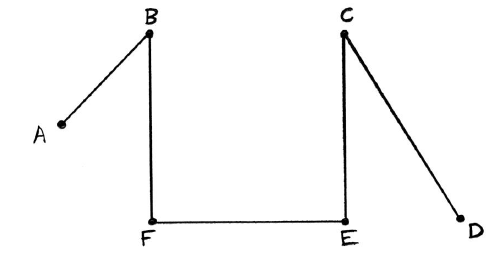
A1
(ii) minimum weight is \(19\) A1
[5 marks]

the shortest path is AFCD A2
the weight is \(16\) A1
[10 marks]
Examiners report
This question was attempted by the majority of students with at least partial success by most. Most candidates were able to give a partial explanation of the condition for a graph to have an Eulerian trail and not an Eulerian circuit, but few were able to provide the required detail. Most candidates were able to write down an Eulerian trail in \(G\). Many candidates successfully applied Kruskal’s algorithm and Dijkstra’s algorithm, but a number of candidates did not appreciate the significance of the order of adding edges in Kruskal’s algorithm, and the explanations of Dijkstra’s algorithm were sometimes poor.
This question was attempted by the majority of students with at least partial success by most. Most candidates were able to give a partial explanation of the condition for a graph to have an Eulerian trail and not an Eulerian circuit, but few were able to provide the required detail. Most candidates were able to write down an Eulerian trail in G. Many candidates successfully applied Kruskal’s algorithm and Dijkstra’s algorithm, but a number of candidates did not appreciate the significance of the order of adding edges in Kruskal’s algorithm, and the explanations of Dijkstra’s algorithm were sometimes poor.
This question was attempted by the majority of students with at least partial success by most. Most candidates were able to give a partial explanation of the condition for a graph to have an Eulerian trail and not an Eulerian circuit, but few were able to provide the required detail. Most candidates were able to write down an Eulerian trail in \(G\). Many candidates successfully applied Kruskal’s algorithm and Dijkstra’s algorithm, but a number of candidates did not appreciate the significance of the order of adding edges in Kruskal’s algorithm, and the explanations of Dijkstra’s algorithm were sometimes poor.

