| Date | May 2016 | Marks available | 2 | Reference code | 16M.2.hl.TZ0.1 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Determine | Question number | 1 | Adapted from | N/A |
Question
Consider the following weighted graph.
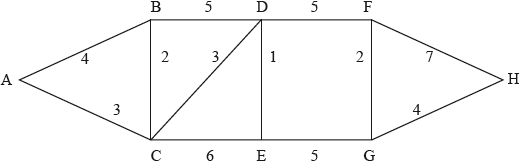
Determine whether or not the graph is Eulerian.
Determine whether or not the graph is Hamiltonian.
Use Kruskal’s algorithm to find a minimum weight spanning tree and state its weight.
Deduce an upper bound for the total weight of a closed walk of minimum weight which visits every vertex.
Explain how the result in part (b) can be used to find a different upper bound and state its value.
Markscheme
the graph is not Eulerian A1
because the graph contains vertices of odd degree R1
[2 marks]
the graph is Hamiltonian A1
because, for example, ABDFHGECA is a Hamiltonian cycle R1
[2 marks]
correctly start to use Kruskal’s algorithm DE(1) (M1)
BC(2), FG(2) or vice-versa A1
DC(3), AC(3) or vice-versa A1
GH(4) (rejecting AB) A1
DF(5) or EG(5) (rejecting BD) A1
total weight \( = 20\) A1
[6 marks]
the minimum weight spanning tree can be traversed twice (M1)
so upper bound is \(2 \times 20 = 40\) A1
[2 marks]
the Hamiltonian cycle found in (b) is a closed walk visiting every vertex and hence can be applied here R1
weight \( = 39\) A1
[2 marks]
Examiners report
(a) and (b) were generally well done. A few candidates said that the graph was not Eulerian because it contained more than two odd vertices. A few candidates failed to back up their assertion that the graph was Hamiltonian by stating an example of a relevant cycle.
(a) and (b) were generally well done. A few candidates said that the graph was not Eulerian because it contained more than two odd vertices. A few candidates failed to back up their assertion that the graph was Hamiltonian by stating an example of a relevant cycle.
In part (c) some candidates did not clearly indicate that they had used Kruskal's algorithm, but just drew a minimum spanning tree.

