| Date | May 2015 | Marks available | 5 | Reference code | 15M.2.sl.TZ2.6 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find and Write down | Question number | 6 | Adapted from | N/A |
Question
The following table shows the number of bicycles, \(x\), produced daily by a factory and their total production cost, \(y\), in US dollars (USD). The table shows data recorded over seven days.
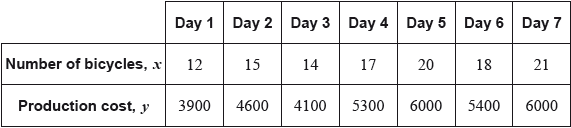
(i) Write down the Pearson’s product–moment correlation coefficient, \(r\), for these data.
(ii) Hence comment on the result.
Write down the equation of the regression line \(y\) on \(x\) for these data, in the form \(y = ax + b\).
Estimate the total cost, to the nearest USD, of producing \(13\) bicycles on a particular day.
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
Explain why the factory does not make a profit when producing \(13\) bicycles on a particular day.
All the bicycles that are produced are sold. The bicycles are sold for 304 USD each.
(i) Write down an expression for the total selling price of \(x\) bicycles.
(ii) Write down an expression for the profit the factory makes when producing \(x\) bicycles on a particular day.
(iii) Find the least number of bicycles that the factory should produce, on a particular day, in order to make a profit.
Markscheme
(i) \(r = 0.985\;\;\;(0.984905 \ldots )\) (G2)
Notes: If unrounded answer is not seen, award (G1)(G0) for \(0.99\) or \(0.984\). Award (G2) for \(0.98\).
(ii) strong, positive (A1)(A1)
\(y = 259.909 \ldots x + 698.648 \ldots \;\;\;(y = 260x + 699)\) (G1)(G1)
Notes: Award (G1) for \(260x\) and (G1) for \(699\). If the answer is not an equation award a maximum of (G1)(G0).
\(y = 259.909 \ldots \times 13 + 698.648 \ldots \) (M1)
Note: Award (M1) for substitution of \(13\) into their regression line equation from part (b).
\(y = 4077.47 \ldots \) (A1)(ft)(G2)
\(y = 4077{\text{ (USD)}}\) (A1)(ft)
Notes: Follow through from their answer to part (b). If rounded values from part (b) used, answer is \(4079\). Award the final (A1)(ft) for a correct rounding to the nearest USD of their answer. The unrounded answer may not be seen.
If answer is \(4077\) and no working is seen, award (G2).
\(13 \times 304 - (4077.47) = - 125.477 \ldots \;\;\;( - 125)\;\;\;\)OR
\(4077.47 - (13 \times 304) = 125.477 \ldots \;\;\;(125)\) (M1)
Notes: Award (M1) for calculating the difference between \(13 \times 304\) and their answer to part (c).
If rounded values are used in equation, answer is \( - 127\).
profit is negative\(\;\;\;\)OR\(\;\;\;{\text{cost}} > {\text{sales}}\) (A1)
OR
\(13 \times 304 = 3952\) (M1)
Note: Award (M1) for calculating the price of \(13\) bikes.
\(3952 < 4077.47\) (A1)(ft)
Note: Award (A1) for showing \(3952\) is less than their part (c). This may be communicated in words. Follow through from part (c), but only if value is greater than \(3952\).
OR
\(\frac{{4077}}{{13}} = 313.62\) (M1)
Note: Award (M1) for calculating the cost of \(1\) bicycle.
\(313.62 > 304\) (A1)(ft)
Note: Award (A1) for showing \(313.62\) is greater than \(304\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(304\).
OR
\(\frac{{4077}}{{304}} = 13.41\) (M1)
Note: Award (M1) for calculating the number of bicycles that should have been be sold to cover total cost.
\(13.41 > 13\) (A1)(ft)
Note: Award (A1) for showing \(13.41\) is greater than \(13\). This may be communicated in words. Follow through from part (c), but only if value is greater than \(13\).
(i) \(304x\) (A1)
(ii) \(304x - (259.909 \ldots x + 698.648 \ldots )\) (A1)(ft)(A1)(ft)
Note: Award (A1)(ft) for difference between their answers to parts (b) and (e)(i), (A1)(ft) for correct expression.
(iii) \(304x - (259.909 \ldots x + 698.648 \ldots ) > 0\) (M1)
Notes: Award (M1) for comparing their expression in part (e)(ii) to \(0\). Accept an equation. Accept \(3040x - y > 0\) or equivalent.
\(x = 16{\text{ bicycles}}\) (A1)(ft)(G2)
Notes: Follow through from their answer to part (b). Answer must be a positive integer greater than \(13\) for the (A1)(ft) to be awarded.
Award (G1) for an answer of \(15.84\).

