| Date | May 2014 | Marks available | 1 | Reference code | 14M.1.sl.TZ2.4 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Write down | Question number | 4 | Adapted from | N/A |
Question
Chocolates in the shape of spheres are sold in boxes of 20.
Each chocolate has a radius of 1 cm.
Find the volume of 1 chocolate.
Write down the volume of 20 chocolates.
The diagram shows the chocolate box from above. The 20 chocolates fit perfectly in the box with each chocolate touching the ones around it or the sides of the box.
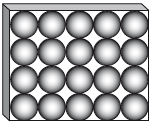
Calculate the volume of the box.
The diagram shows the chocolate box from above. The 20 chocolates fit perfectly in the box with each chocolate touching the ones around it or the sides of the box.
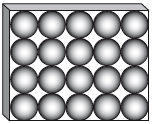
Calculate the volume of empty space in the box.
Markscheme
The first time a correct answer has incorrect or missing units, the final (A1) is not awarded.
\(\frac{4}{3}\pi {(1)^3}\) (M1)
Notes: Award (M1) for correct substitution into correct formula.
\( = 4.19{\text{ }}\left( {{\text{4.18879}} \ldots ,{\text{ }}\frac{4}{3}\pi } \right){\text{ c}}{{\text{m}}^3}\) (A1) (C2)
[2 marks]
The first time a correct answer has incorrect or missing units, the final (A1) is not awarded.
\(83.8{\text{ }}\left( {{\text{83.7758}} \ldots ,{\text{ }}\frac{{80}}{3}\pi } \right){\text{ c}}{{\text{m}}^3}\) (A1)(ft) (C1)
Note: Follow through from their answer to part (a).
[1 mark]
The first time a correct answer has incorrect or missing units, the final (A1) is not awarded.
\(10 \times 8 \times 2\) (M1)
Note: Award (M1) for correct substitution into correct formula.
\( = 160{\text{ c}}{{\text{m}}^3}\) (A1) (C2)
[2 marks]
The first time a correct answer has incorrect or missing units, the final (A1) is not awarded.
\(76.2{\text{ }}\left( {{\text{76.2241}} \ldots ,{\text{ }}\left( {160 - \frac{{80}}{3}\pi } \right)} \right){\text{ c}}{{\text{m}}^3}\) (A1)(ft) (C1)
Note: Follow through from their part (b) and their part (c).
[1 mark]

