| Date | November 2016 | Marks available | 2 | Reference code | 16N.1.sl.TZ0.9 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
The graph of the quadratic function \(f(x) = c + bx - {x^2}\) intersects the \(x\)-axis at the point \({\text{A}}( - 1,{\text{ }}0)\) and has its vertex at the point \({\text{B}}(3,{\text{ }}16)\).
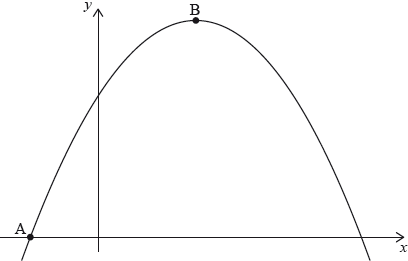
Write down the equation of the axis of symmetry for this graph.
Find the value of \(b\).
Write down the range of \(f(x)\).
Markscheme
\(x = 3\) (A1)(A1) (C2)
Note: Award (A1) for \(x = \) constant, (A1) for the constant being 3.
The answer must be an equation.
[2 marks]
\(\frac{{ - b}}{{2( - 1)}} = 3\) (M1)
Note: Award (M1) for correct substitution into axis of symmetry formula.
OR
\(b - 2x = 0\) (M1)
Note: Award (M1) for correctly differentiating and equating to zero.
OR
\(c + b( - 1) - {( - 1)^2} = 0\) (or equivalent)
\(c + b(3) - {(3)^2} = 16\) (or equivalent) (M1)
Note: Award (M1) for correct substitution of \(( - 1,{\text{ }}0)\) and \((3,{\text{ }}16)\) in the original quadratic function.
\((b = ){\text{ }}6\) (A1)(ft) (C2)
Note: Follow through from part (a).
[2 marks]
\(( - \infty ,{\text{ 16]}}\) OR \(] - \infty ,{\text{ }}16]\) (A1)(A1)
Note: Award (A1) for two correct interval endpoints, (A1) for left endpoint excluded and right endpoint included.
[2 marks]

